Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre sólidos geométricos.
Mapa Mental sobre sólidos geométricos (1)

Mapa Mental sobre sólidos geométricos (2)
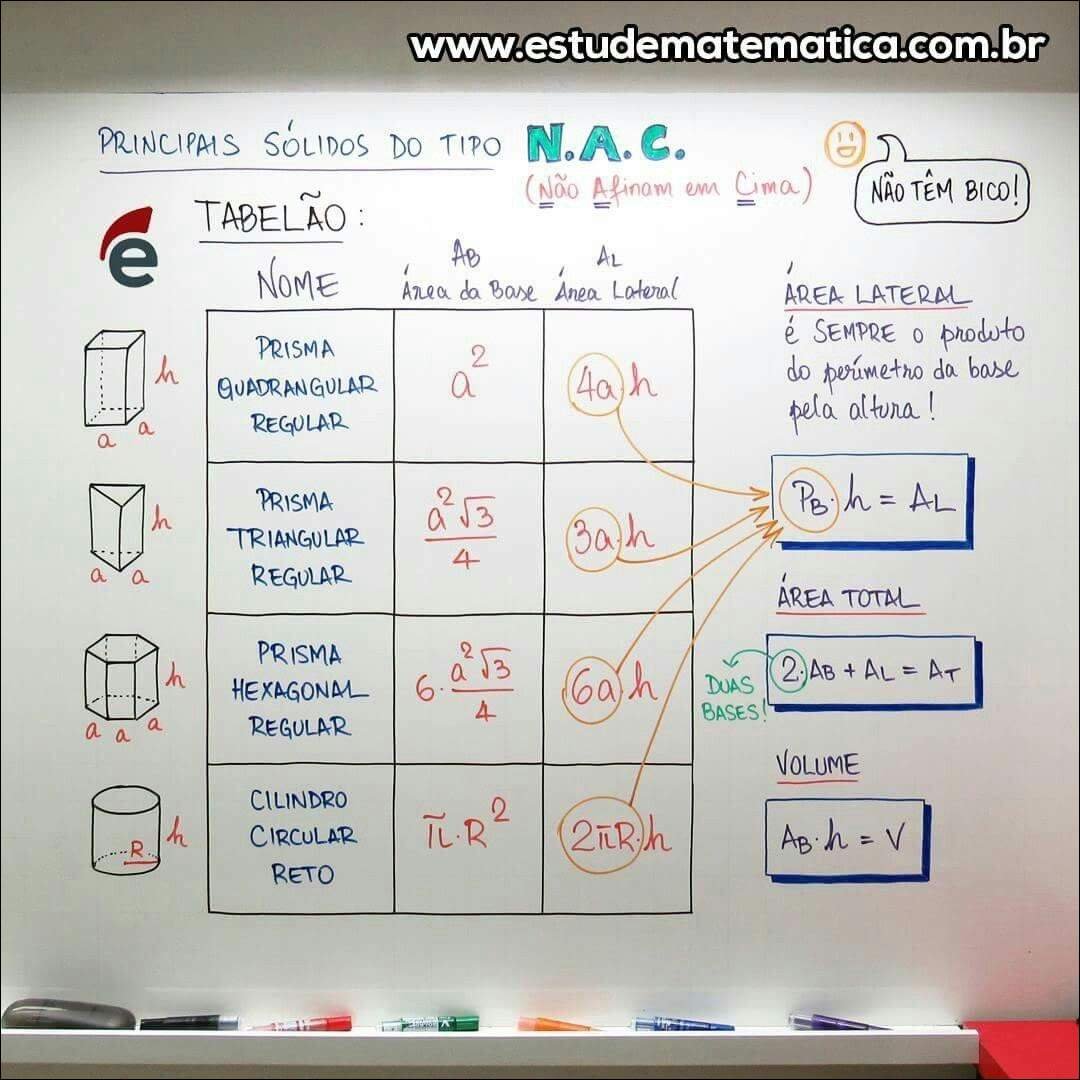
Mapa Mental sobre sólidos geométricos (3)
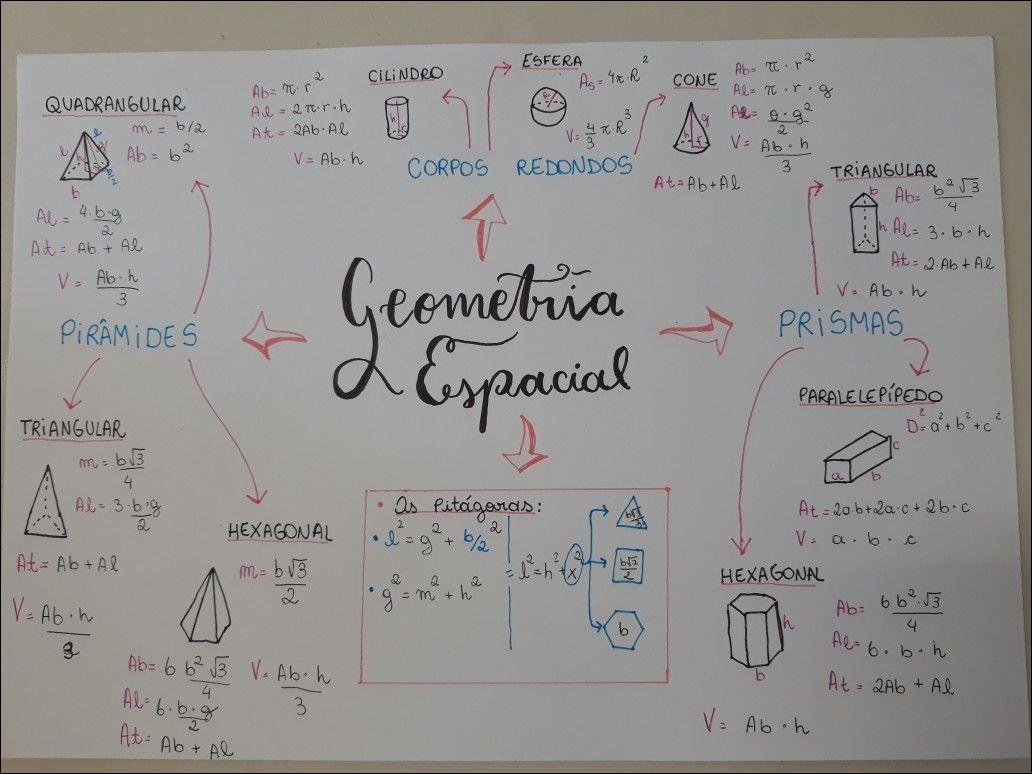
Mapa Mental sobre sólidos geométricos (4)
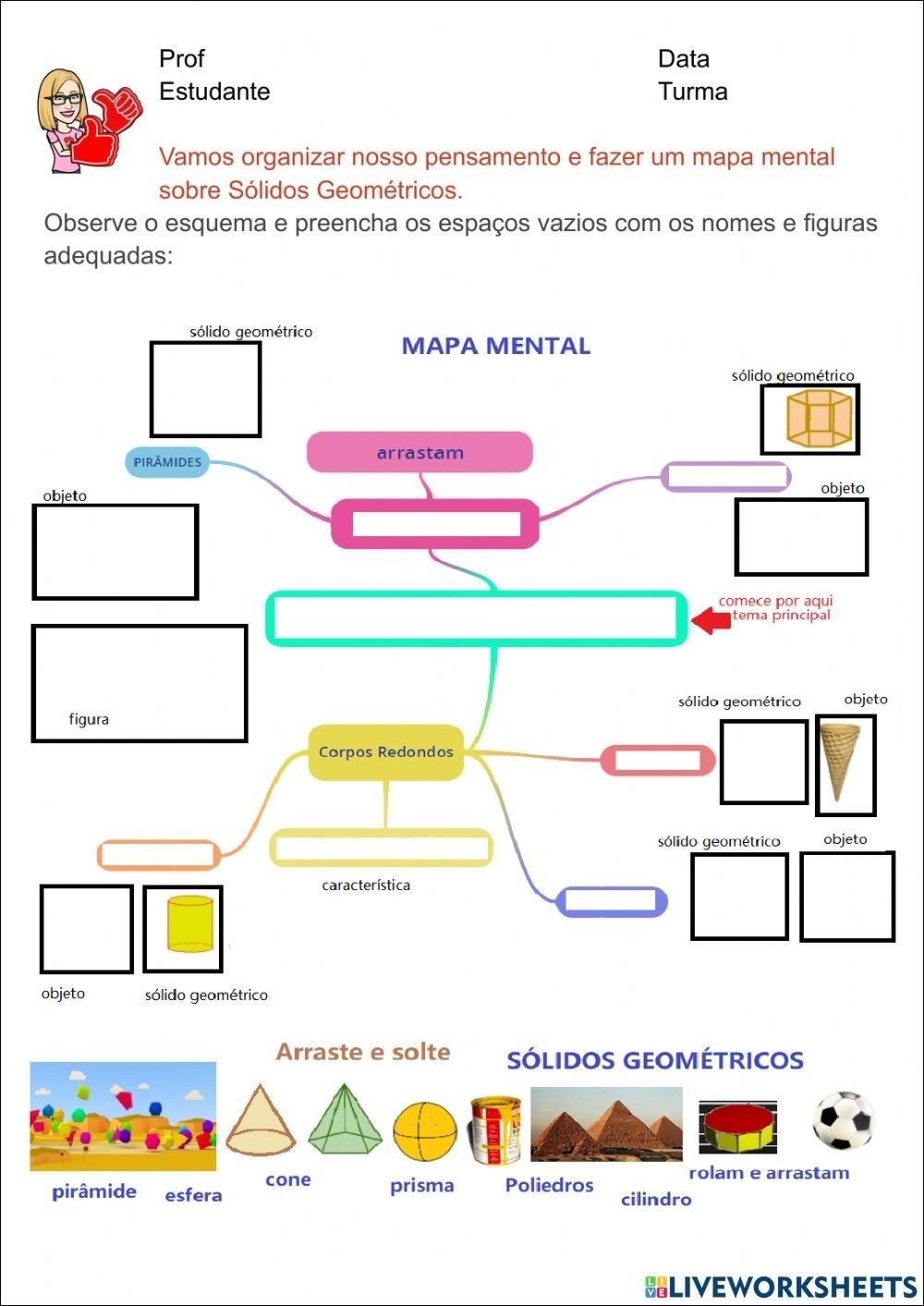
Mapa Mental sobre sólidos geométricos (5)
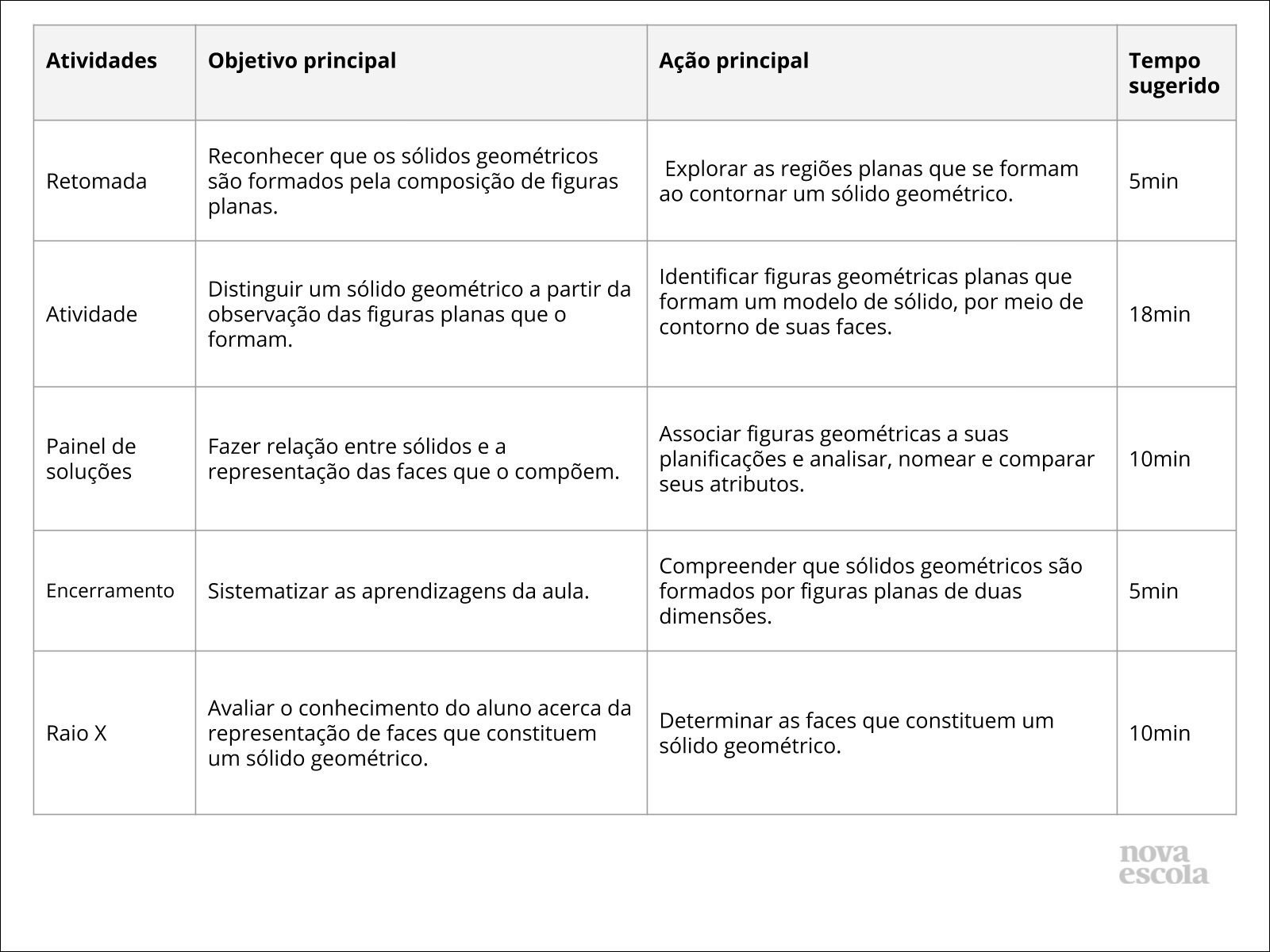
Mapa Mental sobre sólidos geométricos (6)

Mapa Mental sobre sólidos geométricos (7)

Mapa Mental sobre sólidos geométricos (8)
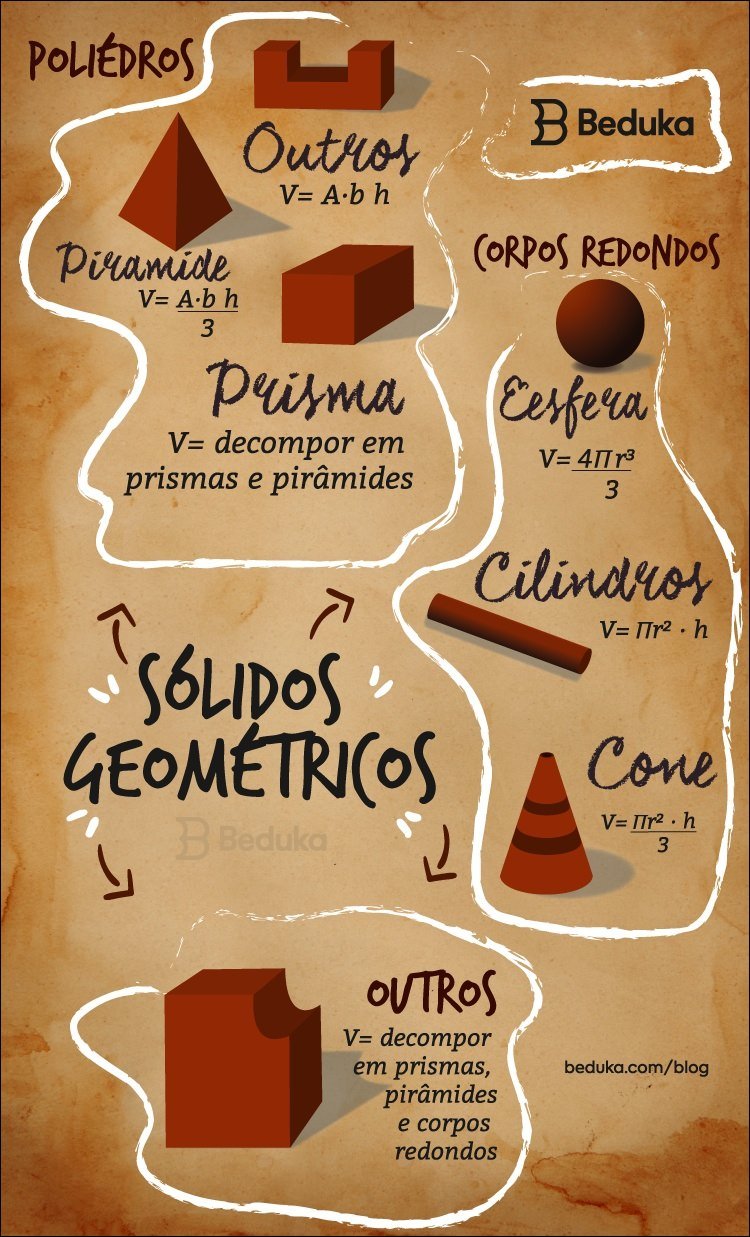
Mapa Mental sobre sólidos geométricos (9)

Mapa Mental sobre sólidos geométricos (10)

Mapa Mental sobre sólidos geométricos (11)
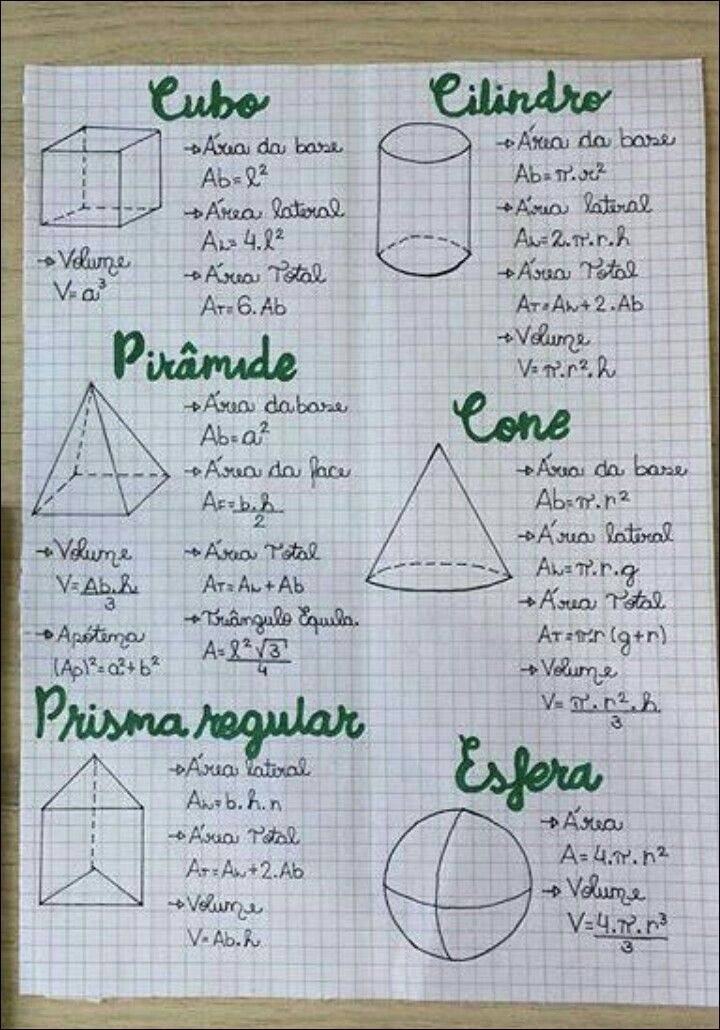
Mapa Mental sobre sólidos geométricos (12)

Mapa Mental sobre sólidos geométricos (13)

Resumo sobre sólidos geométricos
Os sólidos geométricos são figuras tridimensionais que ocupam um volume no espaço. Eles são caracterizados por terem comprimento, largura e altura, e são classificados em duas categorias principais: poliedros e corpos redondos.
Os poliedros são sólidos delimitados por polígonos planos. Eles podem ser regulares, como o cubo (formado por seis quadrados iguais) e o tetraedro (formado por quatro triângulos equiláteros), ou irregulares. A relação de Euler, V – A + F = 2 (onde V = vértices, A = arestas e F = faces), é uma importante ferramenta para analisar as propriedades dos poliedros.
Os corpos redondos são sólidos que possuem superfícies curvas, resultantes da rotação de figuras planas. Exemplos incluem o cilindro (resultante da rotação de um retângulo), o cone (resultante da rotação de um triângulo retângulo) e a esfera (resultante da rotação de um círculo). Eles se diferenciam dos poliedros pela ausência de faces planas e pela presença de superfícies curvas.
O estudo dos sólidos geométricos é fundamental em diversas áreas, como arquitetura, engenharia, design e artes. O conhecimento de suas propriedades, como volume, área da superfície e relações angulares, permite o cálculo de materiais, a compreensão da estrutura de objetos tridimensionais e a resolução de problemas práticos. A compreensão dessas figuras é essencial para a visualização espacial e o desenvolvimento do raciocínio geométrico.
