Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre vetor.
Mapa Mental sobre vetor (1)
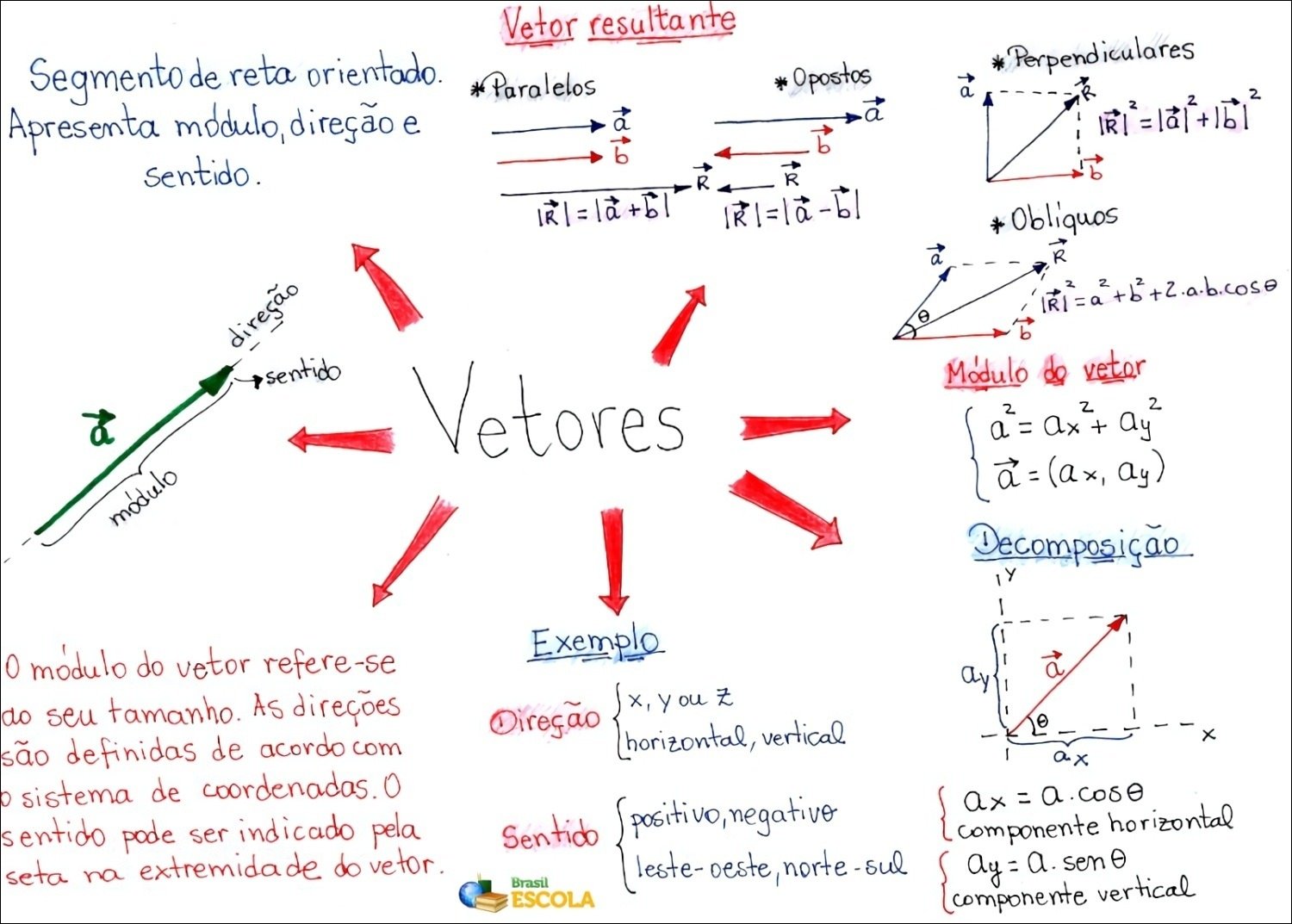
Mapa Mental sobre vetor (2)

Mapa Mental sobre vetor (3)
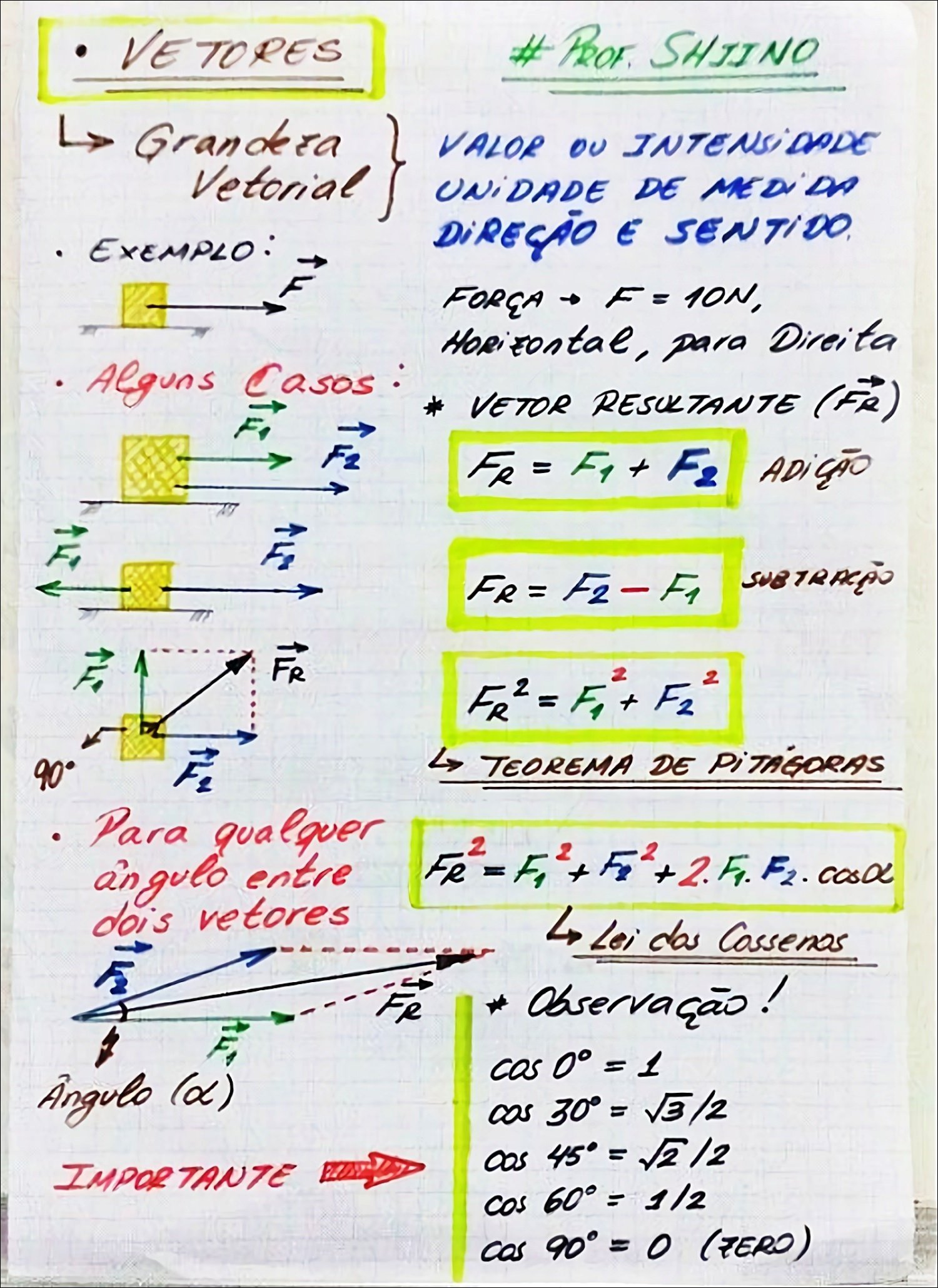
Mapa Mental sobre vetor (4)

Mapa Mental sobre vetor (5)
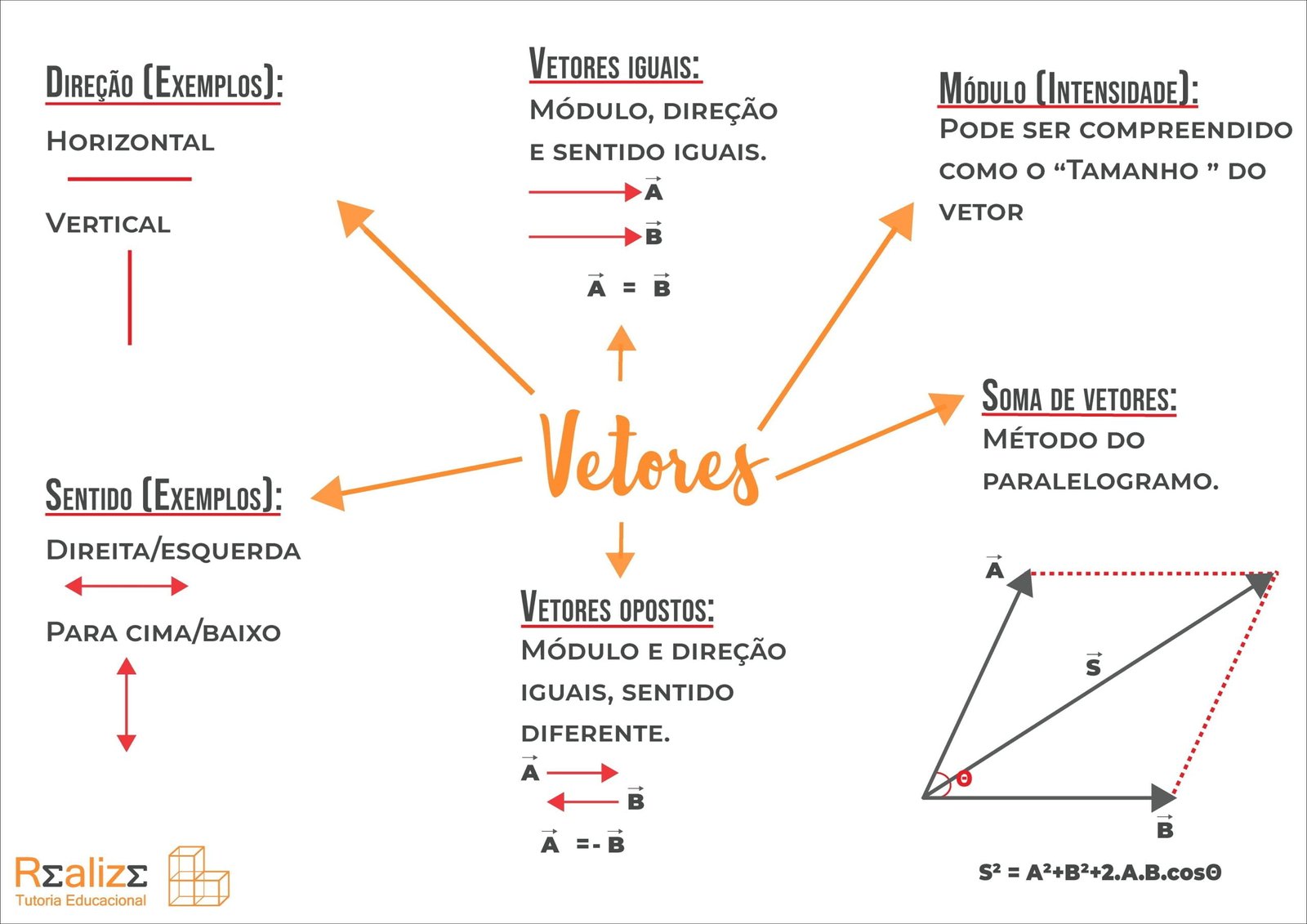
Mapa Mental sobre vetor (6)
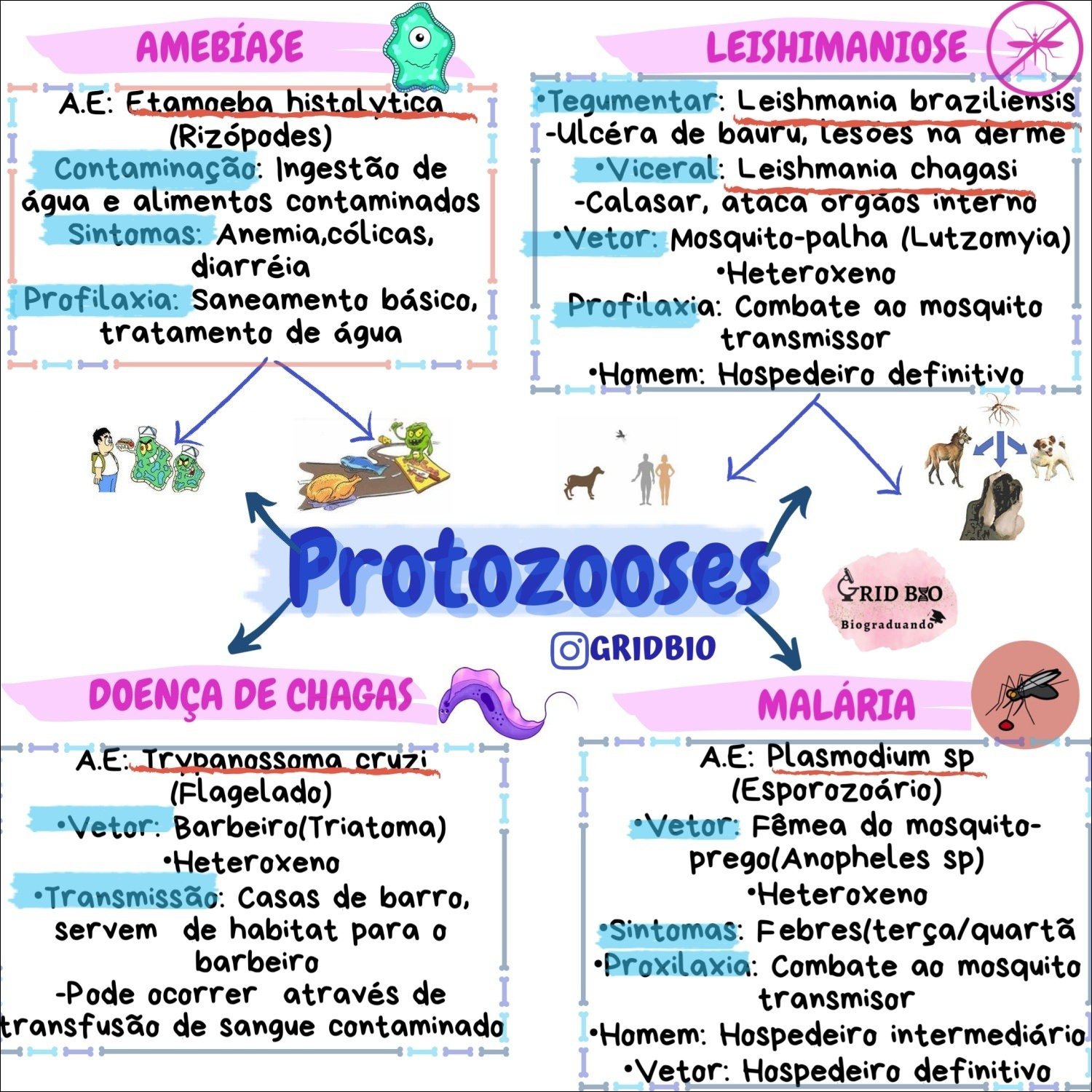
Mapa Mental sobre vetor (7)

Mapa Mental sobre vetor (8)

Mapa Mental sobre vetor (9)
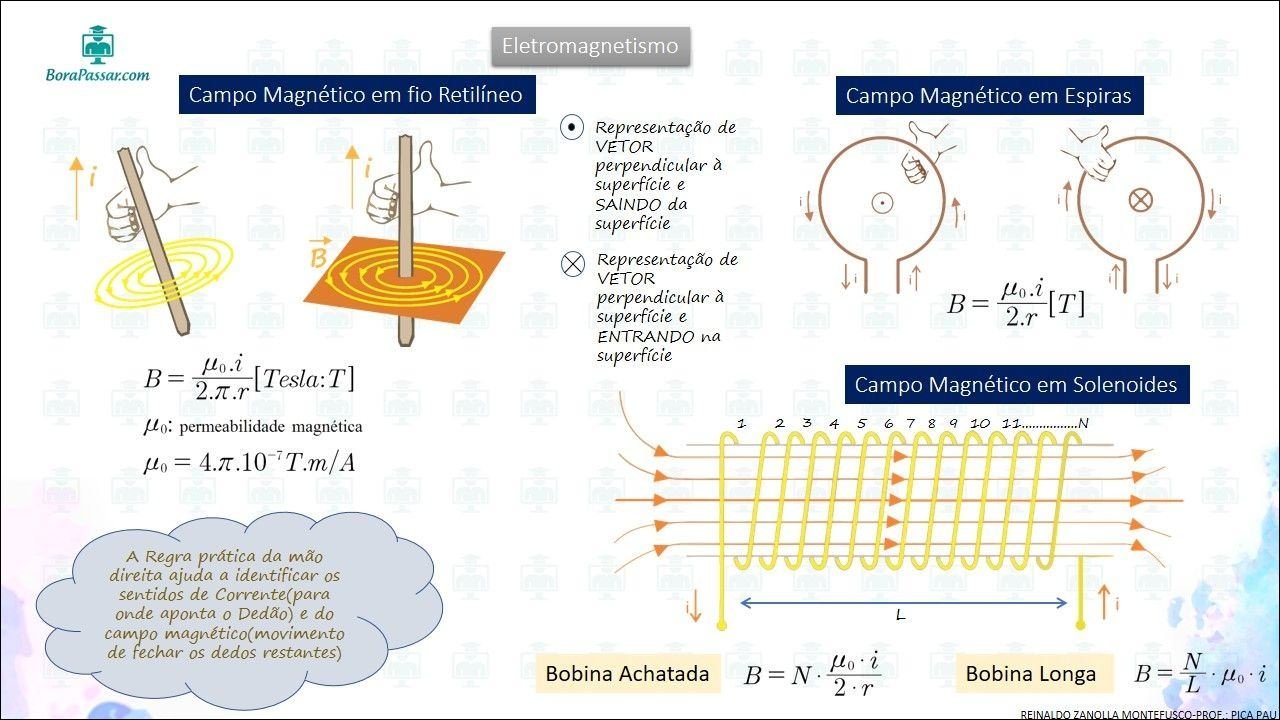
Mapa Mental sobre vetor (10)
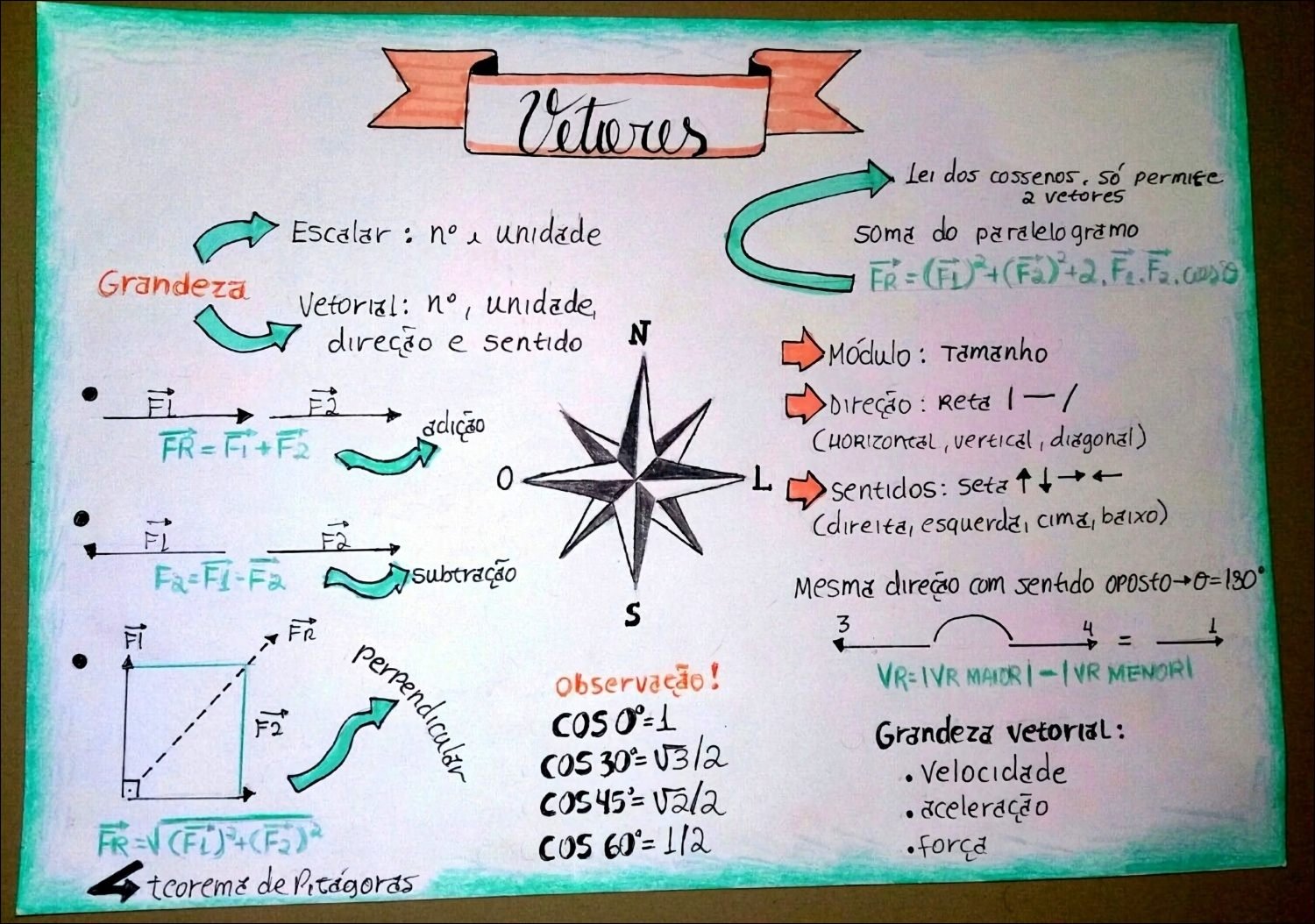
Mapa Mental sobre vetor (11)

Mapa Mental sobre vetor (12)

Mapa Mental sobre vetor (13)

Mapa Mental sobre vetor (14)

Mapa Mental sobre vetor (15)

Mapa Mental sobre vetor (16)

Mapa Mental sobre vetor (17)

Mapa Mental sobre vetor (18)

Mapa Mental sobre vetor (19)
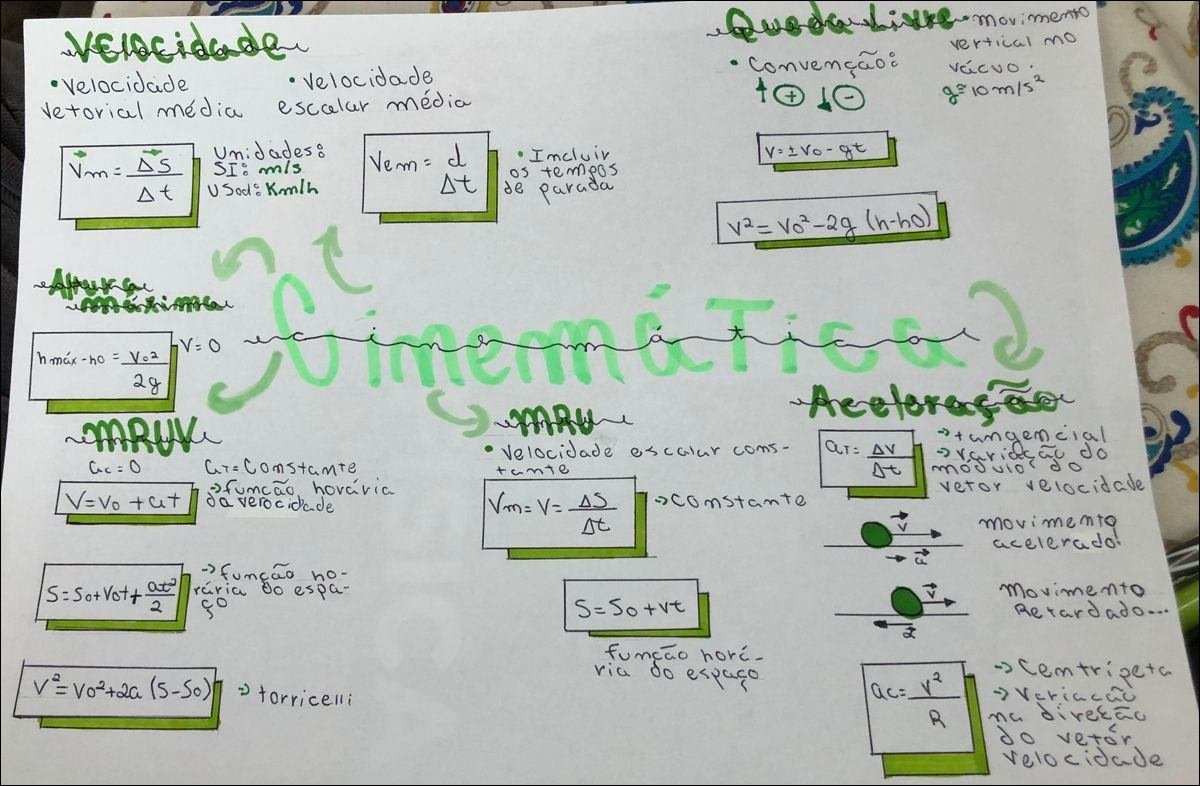
Mapa Mental sobre vetor (20)
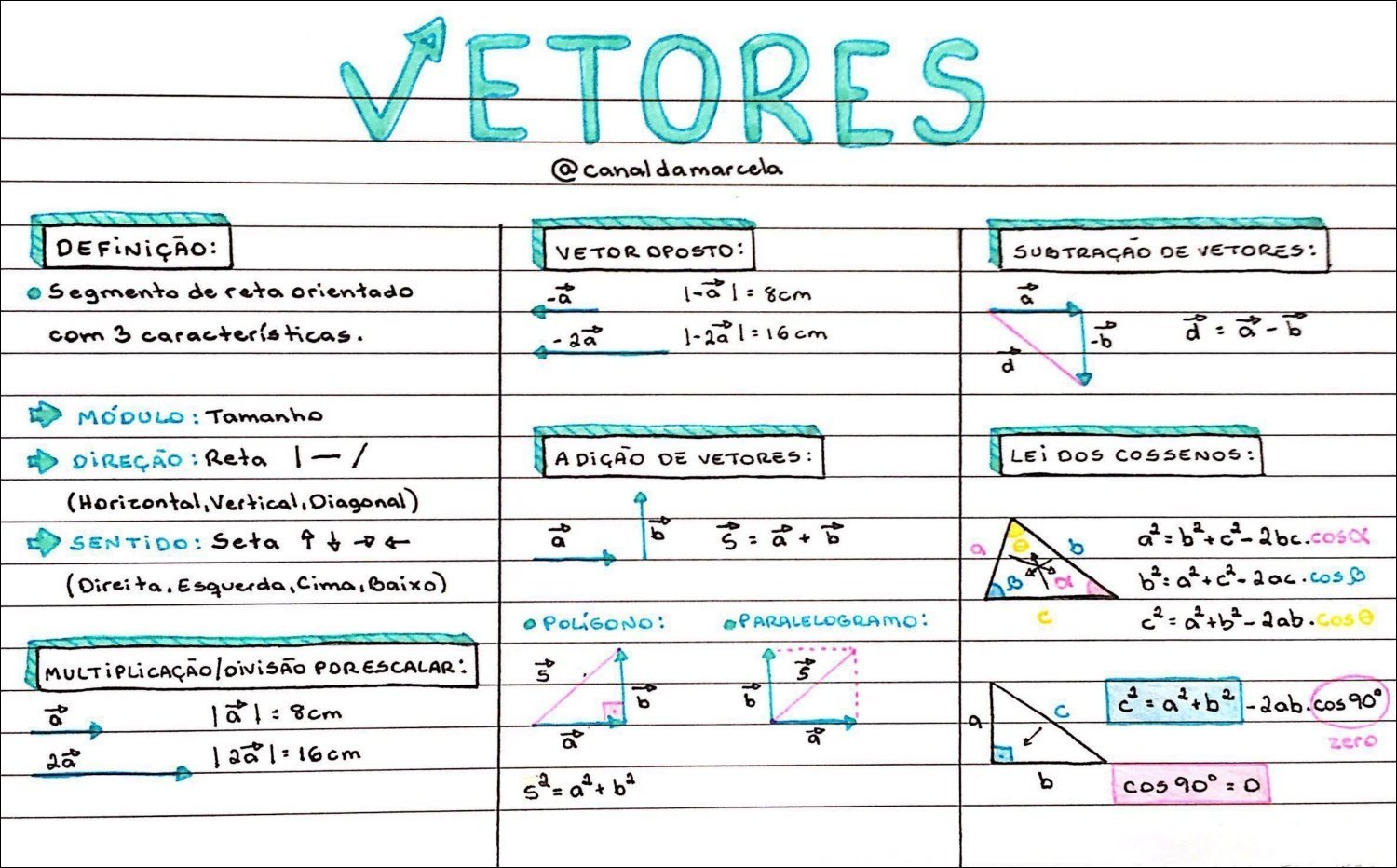
Resumo sobre vetor
Um vetor, em física e matemática, é um conceito fundamental que representa tanto uma magnitude (tamanho ou intensidade) quanto uma direção. Diferente de uma escalar, que possui apenas magnitude (como temperatura ou massa), um vetor descreve algo que tem direção e sentido, como a velocidade de um carro (que possui velocidade e direção) ou a força aplicada em um objeto (que possui intensidade e direção).
Vetor pode ser representado de diversas formas, a mais comum é através de uma seta, onde o comprimento da seta indica a magnitude e a ponta da seta aponta na direção do vetor. Além disso, vetores podem ser expressos em forma de componentes, especialmente em sistemas de coordenadas cartesianas (x, y, z). Cada componente representa a projeção do vetor em uma direção específica.
As operações vetoriais são essenciais para manipular e combinar vetores. Algumas operações comuns incluem a soma (que combina vetores para obter um vetor resultante), a subtração, a multiplicação por um escalar (que altera a magnitude do vetor) e o produto escalar e vetorial (que resultam em escalares e vetores, respectivamente, e são usados para calcular ângulos e áreas/volumes).
A compreensão de vetores é crucial em diversas áreas da ciência e engenharia, incluindo física (mecânica, eletromagnetismo), computação gráfica, robótica e navegação, pois permite modelar e analisar fenômenos que envolvem direção e magnitude. Dominar os conceitos e operações vetoriais é, portanto, essencial para uma análise precisa e abrangente desses fenômenos.
