Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre Polinômios.
Mapa Mental sobre Polinômios (1)
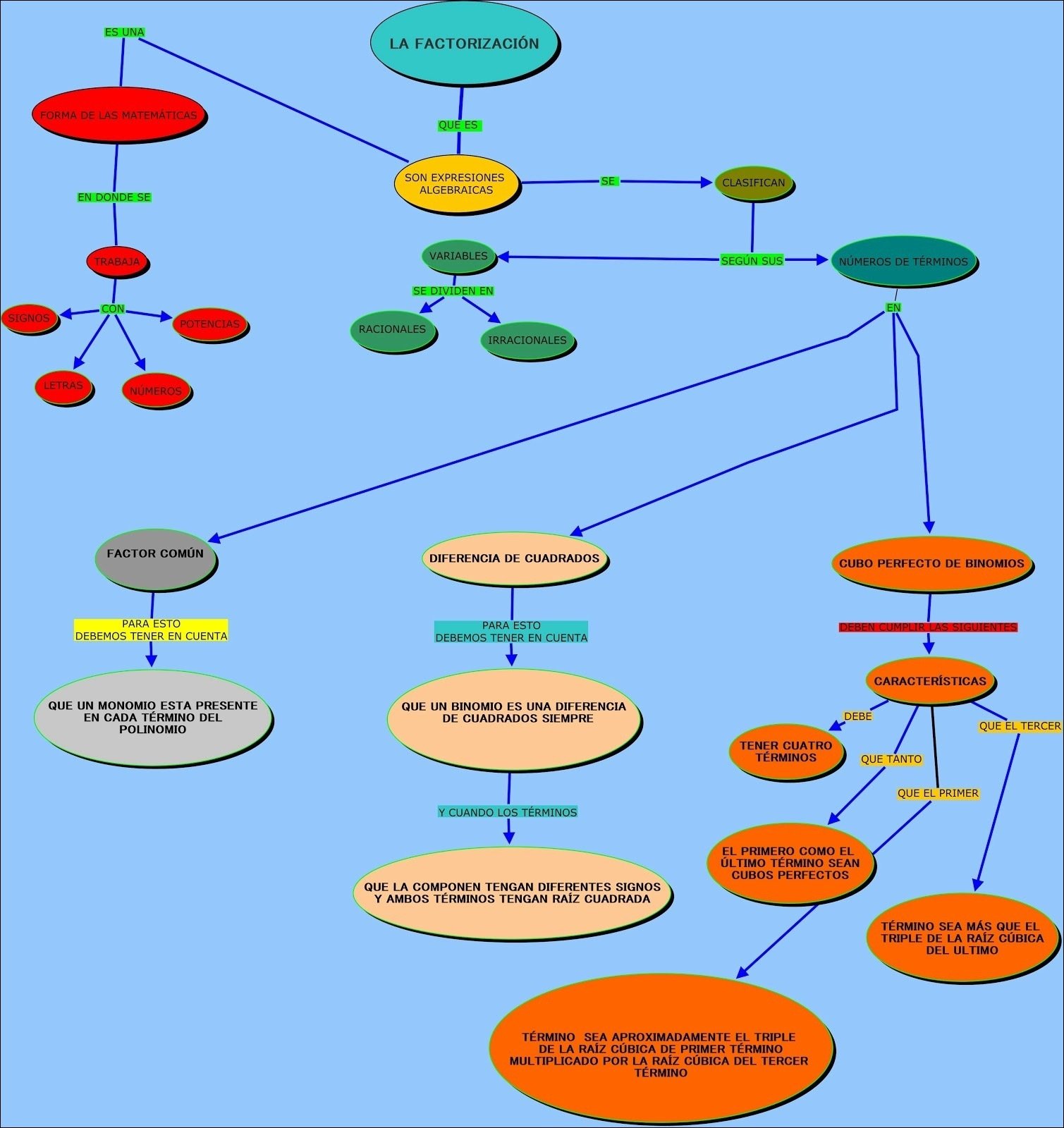
Mapa Mental sobre Polinômios (2)

Mapa Mental sobre Polinômios (3)

Mapa Mental sobre Polinômios (4)

Mapa Mental sobre Polinômios (5)

Mapa Mental sobre Polinômios (6)
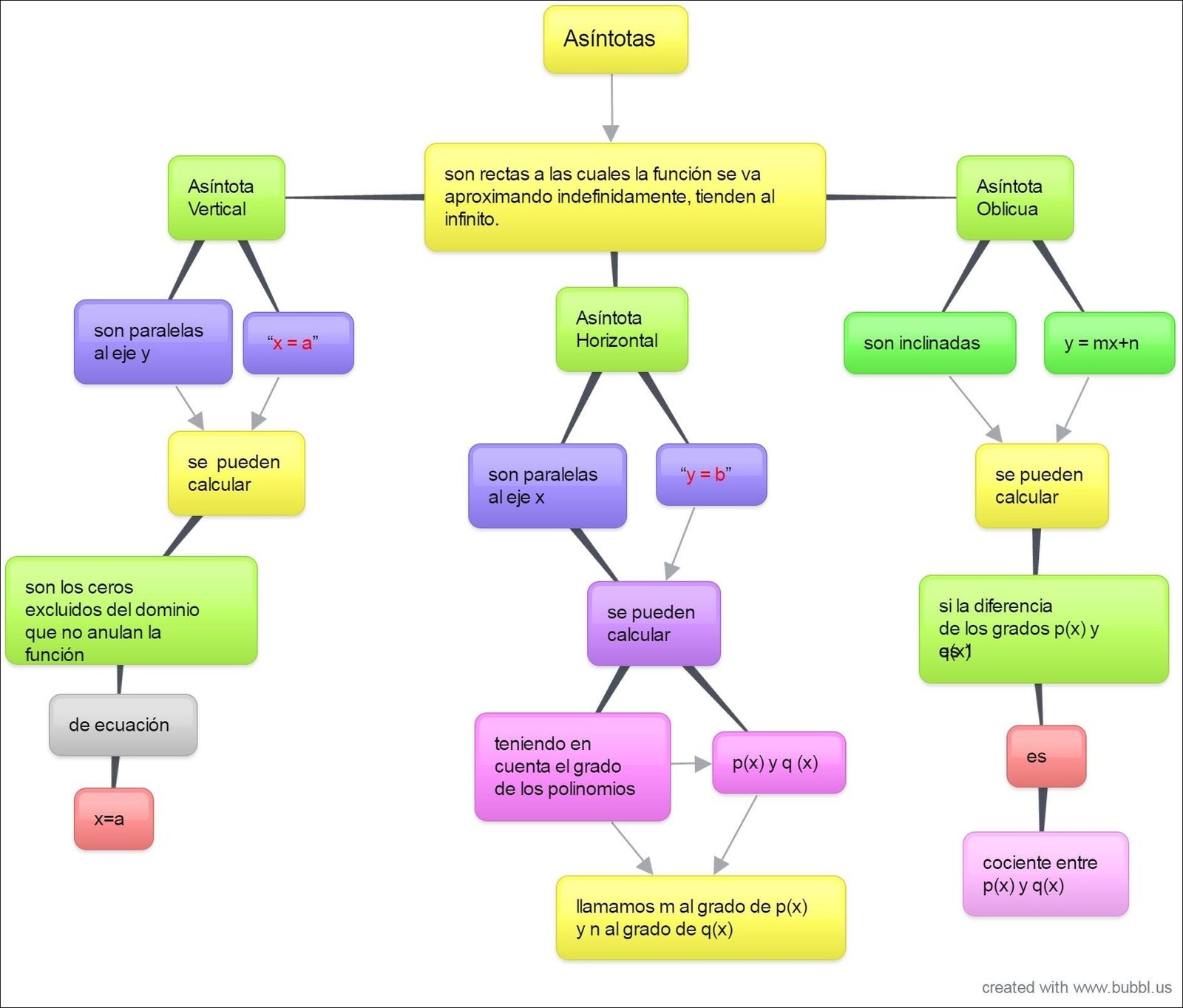
Mapa Mental sobre Polinômios (7)
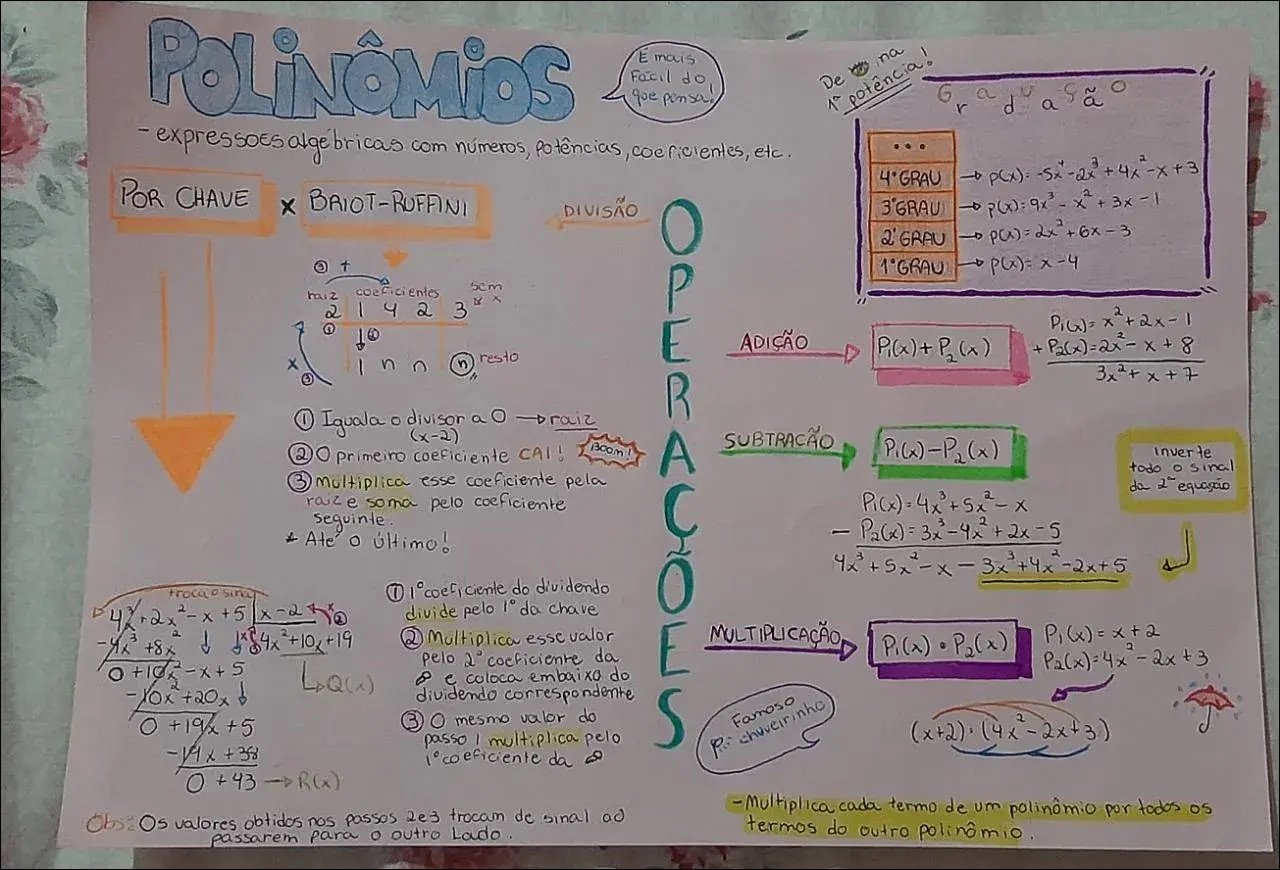
Mapa Mental sobre Polinômios (8)
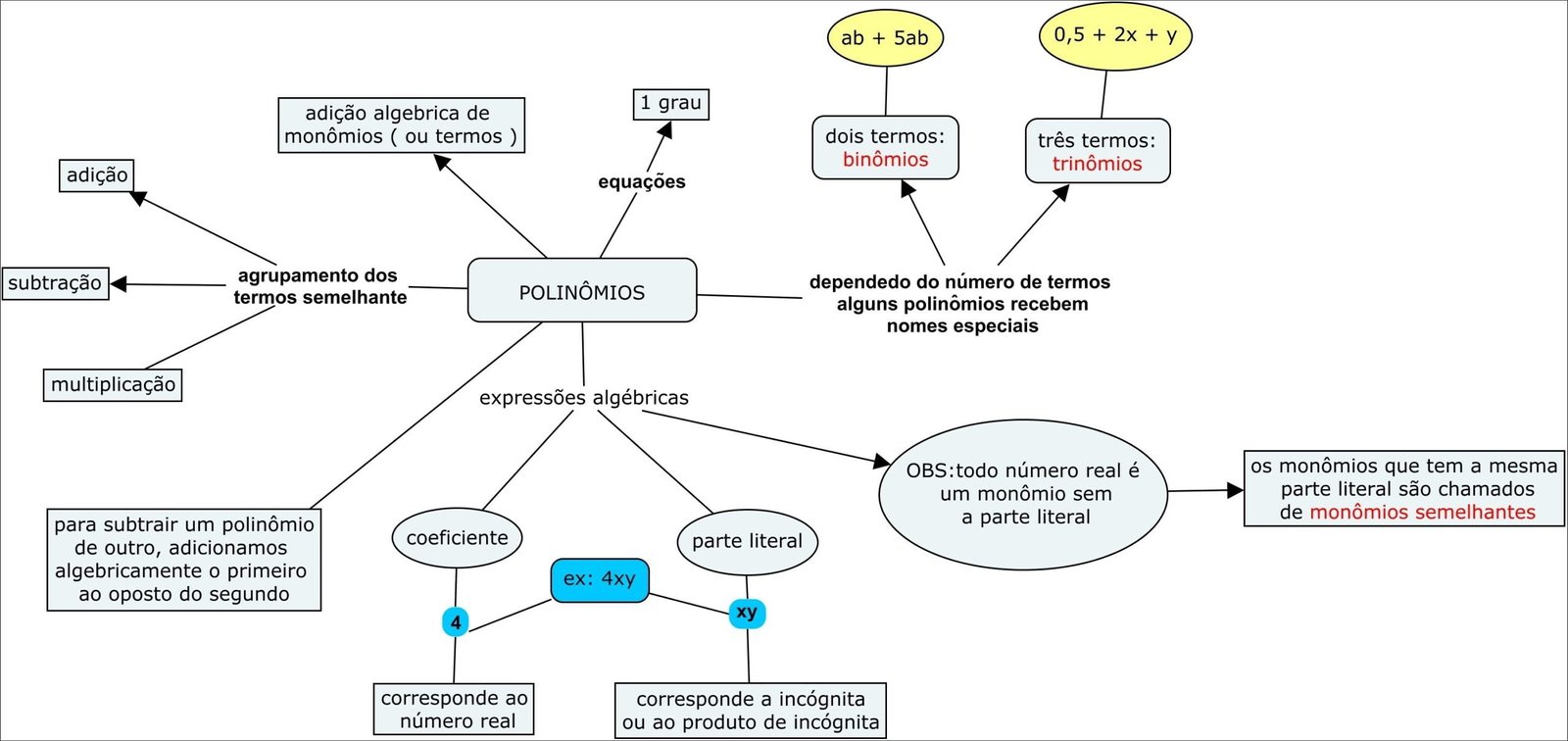
Mapa Mental sobre Polinômios (9)
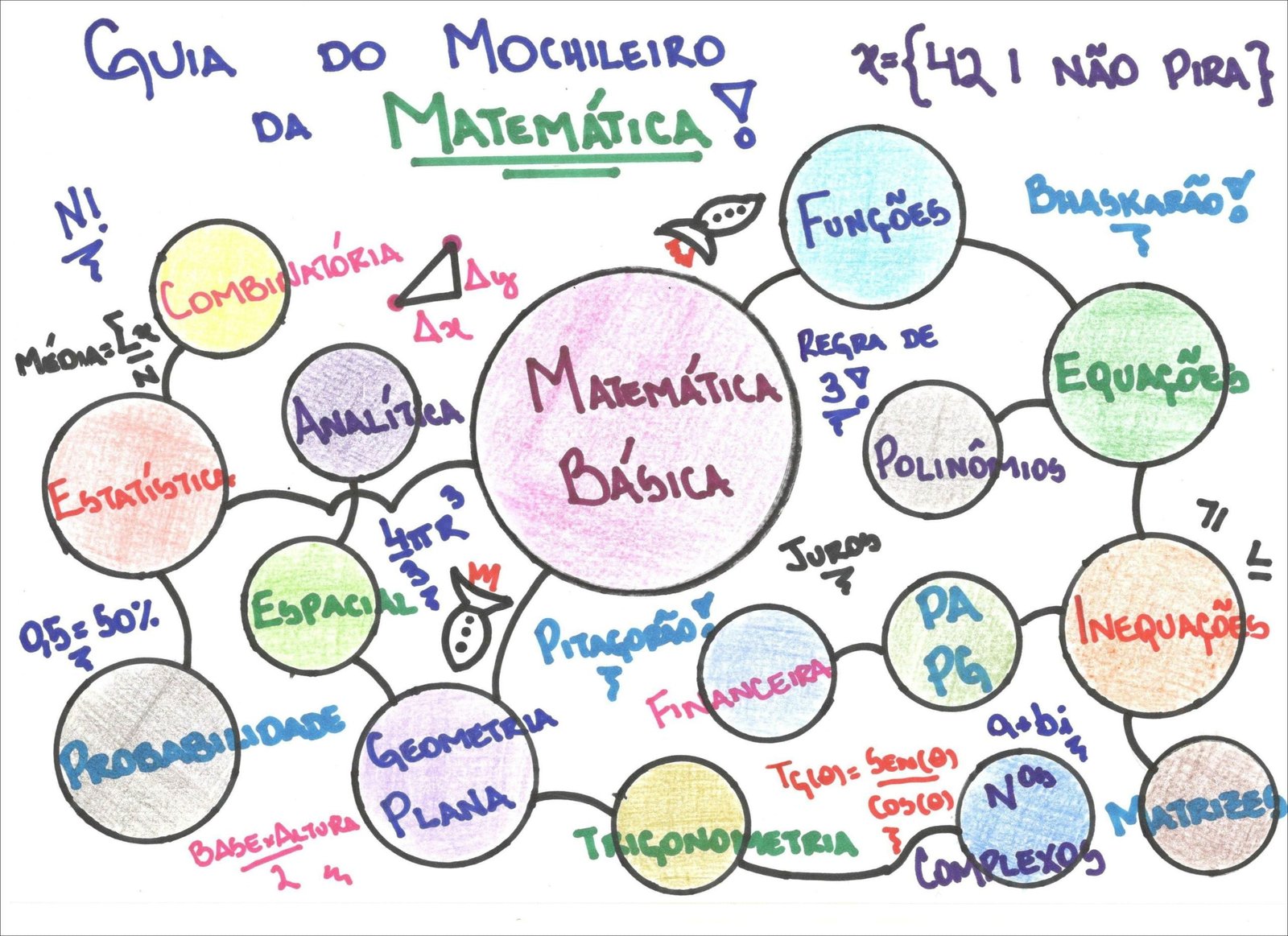
Mapa Mental sobre Polinômios (10)

Mapa Mental sobre Polinômios (11)
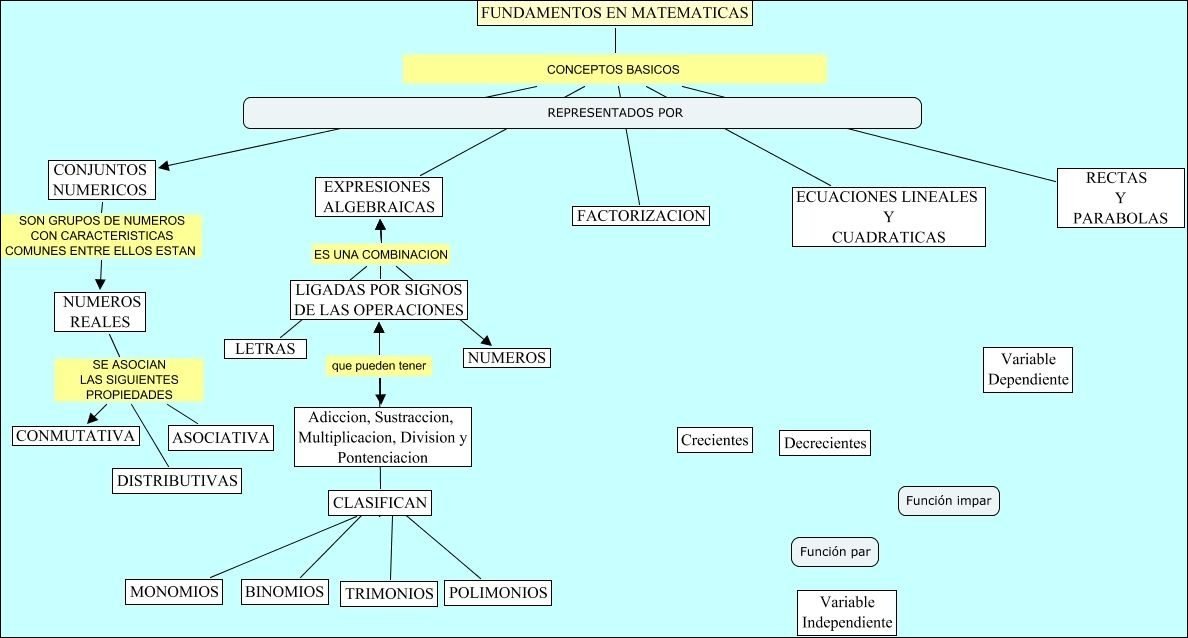
Mapa Mental sobre Polinômios (12)

Mapa Mental sobre Polinômios (13)

Mapa Mental sobre Polinômios (14)

Mapa Mental sobre Polinômios (15)
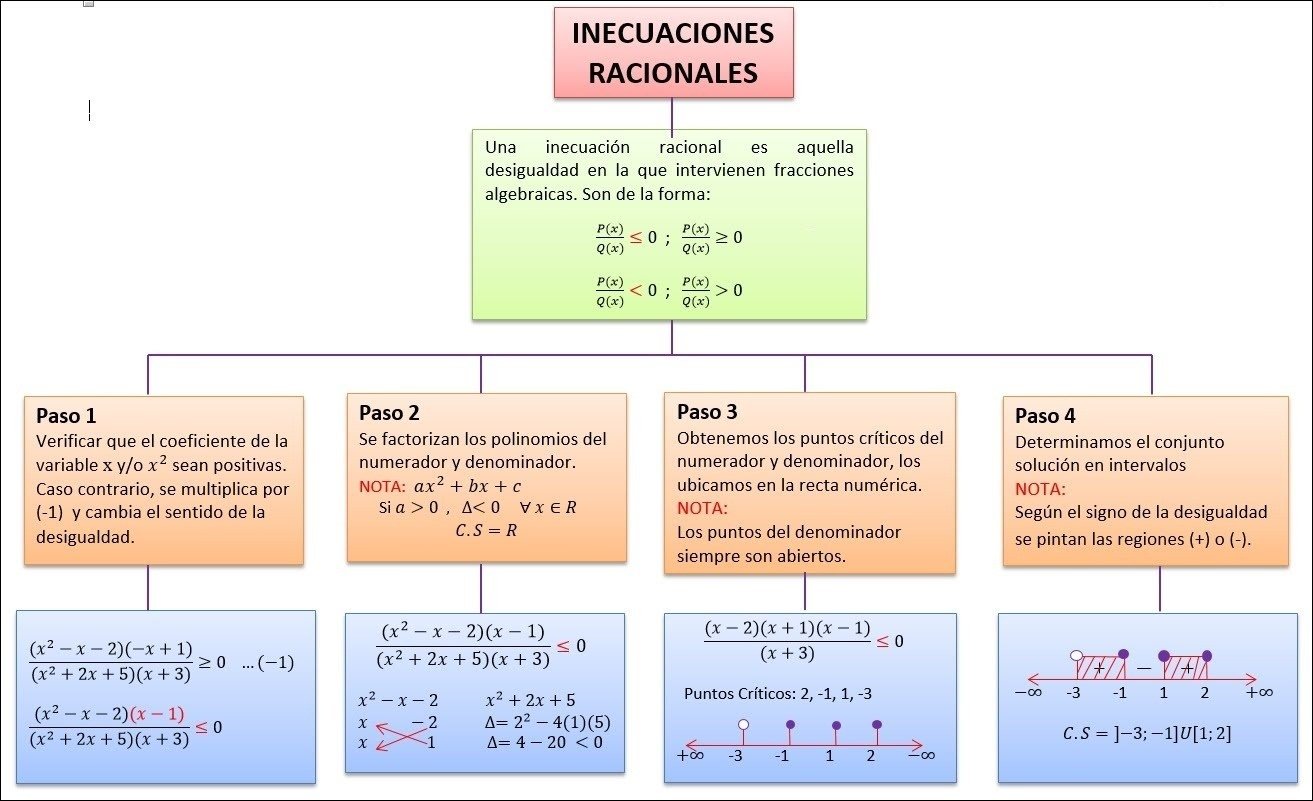
Mapa Mental sobre Polinômios (16)
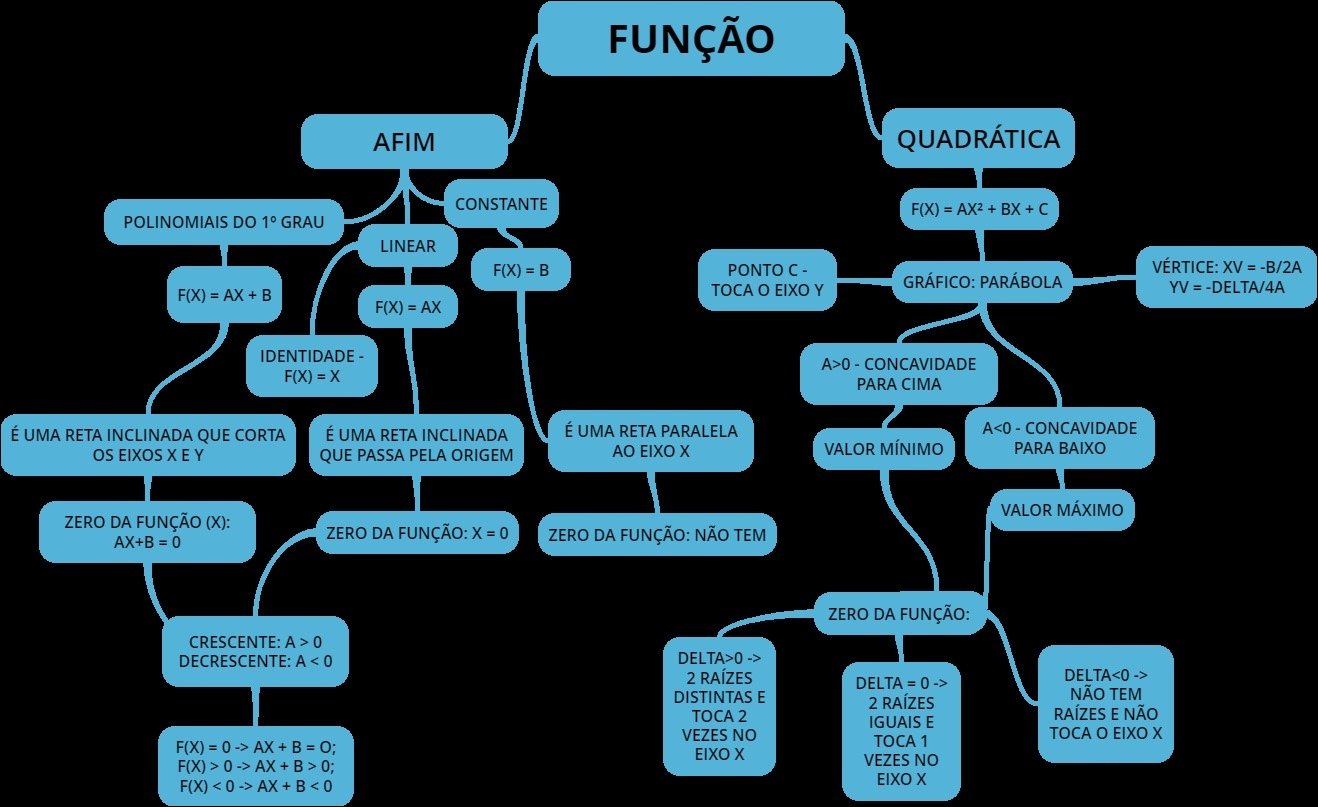
Mapa Mental sobre Polinômios (17)

Mapa Mental sobre Polinômios (18)

Mapa Mental sobre Polinômios (19)
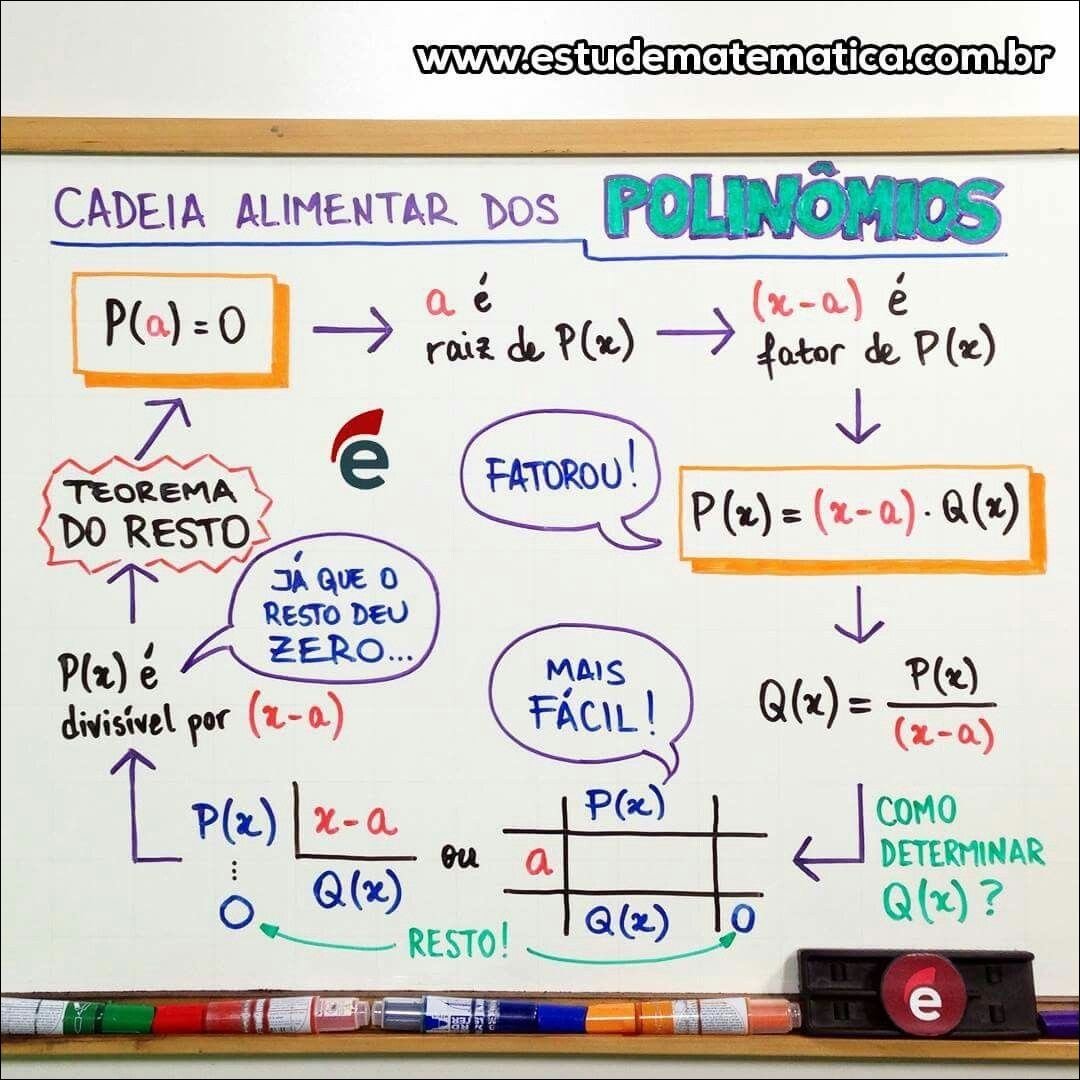
Mapa Mental sobre Polinômios (20)

Resumo sobre Polinômios
Polinômios são expressões matemáticas compostas por variáveis e constantes, combinadas por operações de adição, subtração, multiplicação e exponenciação de expoentes inteiros não negativos. A forma geral de um polinômio em uma variável, x, é anxn + an-1xn-1 + … + a1x + a0, onde ai são coeficientes e n é o grau do polinômio.
Os termos de um polinômio são separados por sinais de adição ou subtração. O termo de maior grau determina o grau do polinômio, o qual influencia seu comportamento. Polinômios são fundamentais em diversas áreas da matemática e ciências, sendo utilizados para modelar e resolver problemas em física, engenharia, economia e outras disciplinas.
Algumas operações importantes com polinômios incluem: adição, subtração, multiplicação, e divisão. A multiplicação de polinômios envolve a multiplicação de cada termo de um polinômio por cada termo do outro, seguida da simplificação dos termos semelhantes. A divisão de polinômios pode ser feita por métodos como a divisão longa.
Polinômios também possuem raízes, ou zeros, que são os valores de x para os quais o valor do polinômio é zero. O Teorema Fundamental da Álgebra garante que todo polinômio de grau n possui exatamente n raízes complexas (contando multiplicidades), e técnicas como a fatoração podem ser usadas para encontrar essas raízes.
