Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre Função quadrática.
Mapa Mental sobre Função quadrática (1)

Mapa Mental sobre Função quadrática (2)
Mapa Mental sobre Função quadrática (3)

Mapa Mental sobre Função quadrática (4)

Mapa Mental sobre Função quadrática (5)
Mapa Mental sobre Função quadrática (6)
Mapa Mental sobre Função quadrática (7)
Mapa Mental sobre Função quadrática (8)
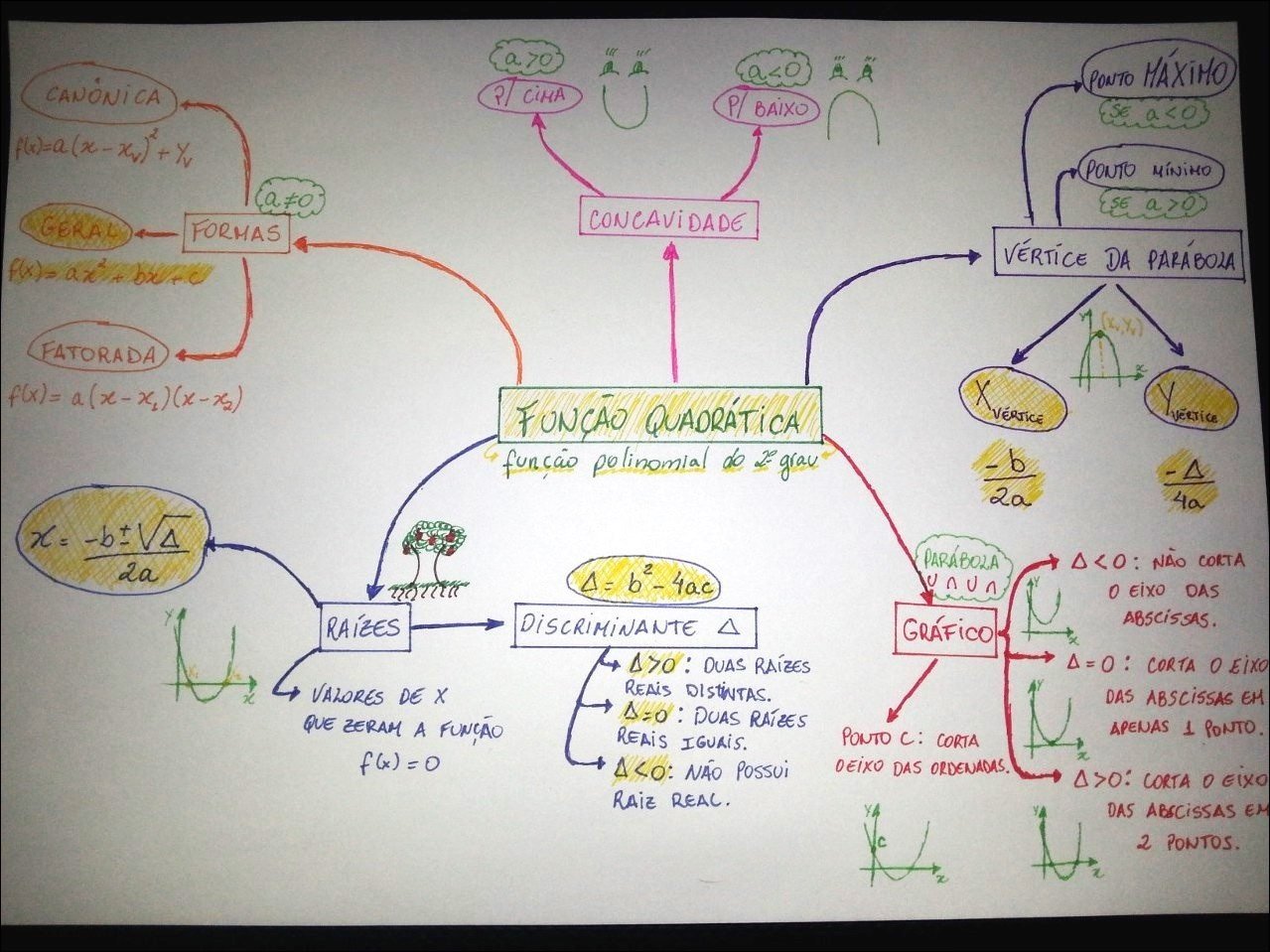
Mapa Mental sobre Função quadrática (9)

Mapa Mental sobre Função quadrática (10)

Mapa Mental sobre Função quadrática (11)

Mapa Mental sobre Função quadrática (12)

Mapa Mental sobre Função quadrática (13)
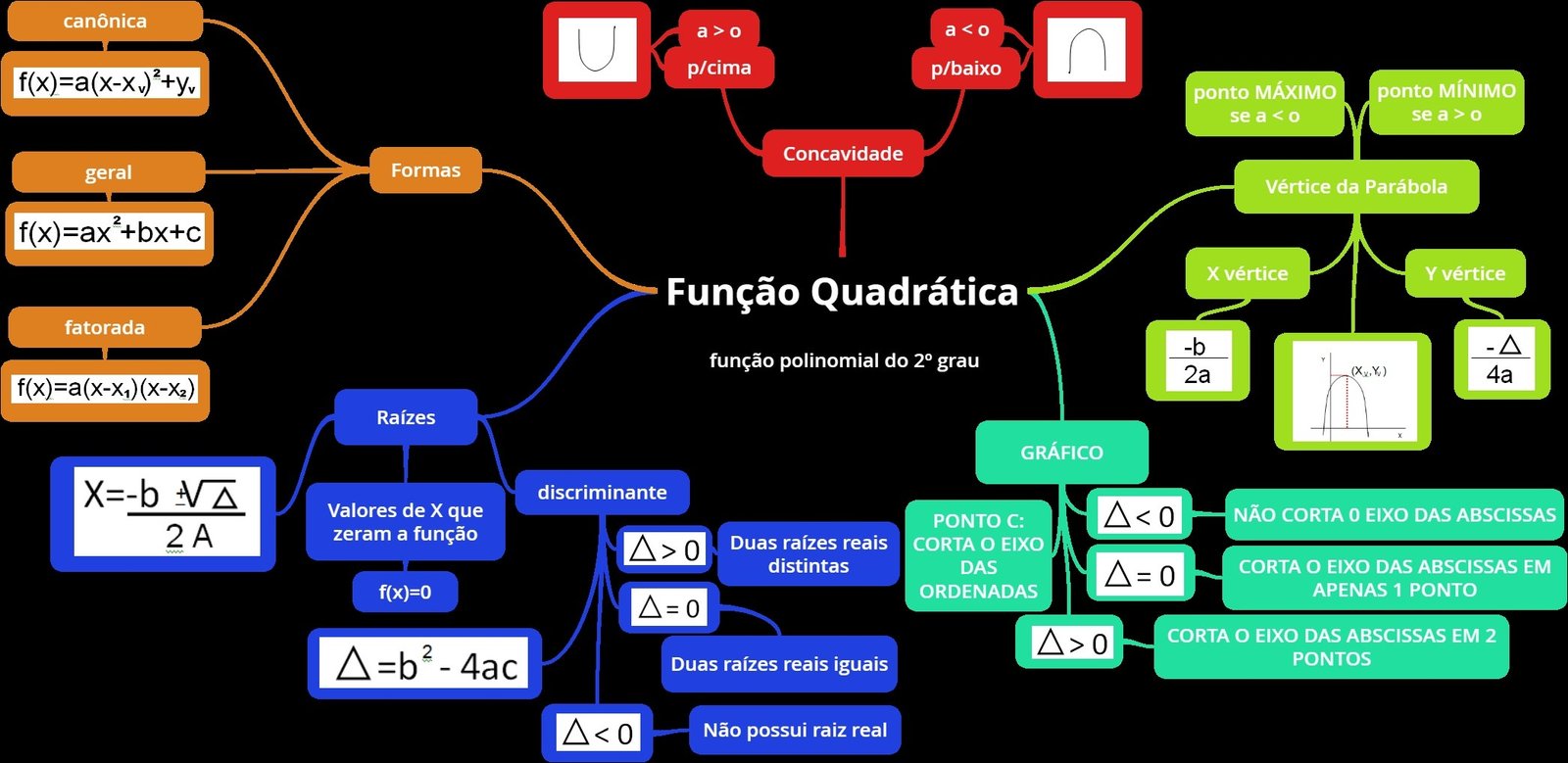
Mapa Mental sobre Função quadrática (14)

Mapa Mental sobre Função quadrática (15)

Mapa Mental sobre Função quadrática (16)

Mapa Mental sobre Função quadrática (17)

Mapa Mental sobre Função quadrática (18)
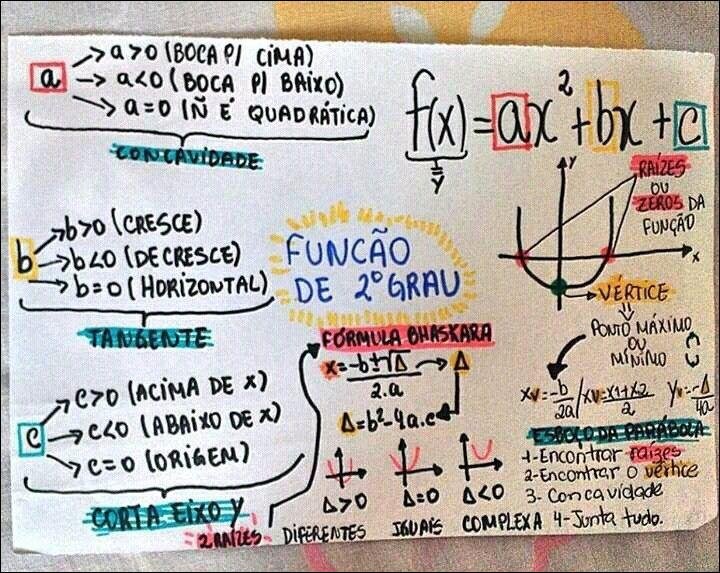
Mapa Mental sobre Função quadrática (19)

Mapa Mental sobre Função quadrática (20)
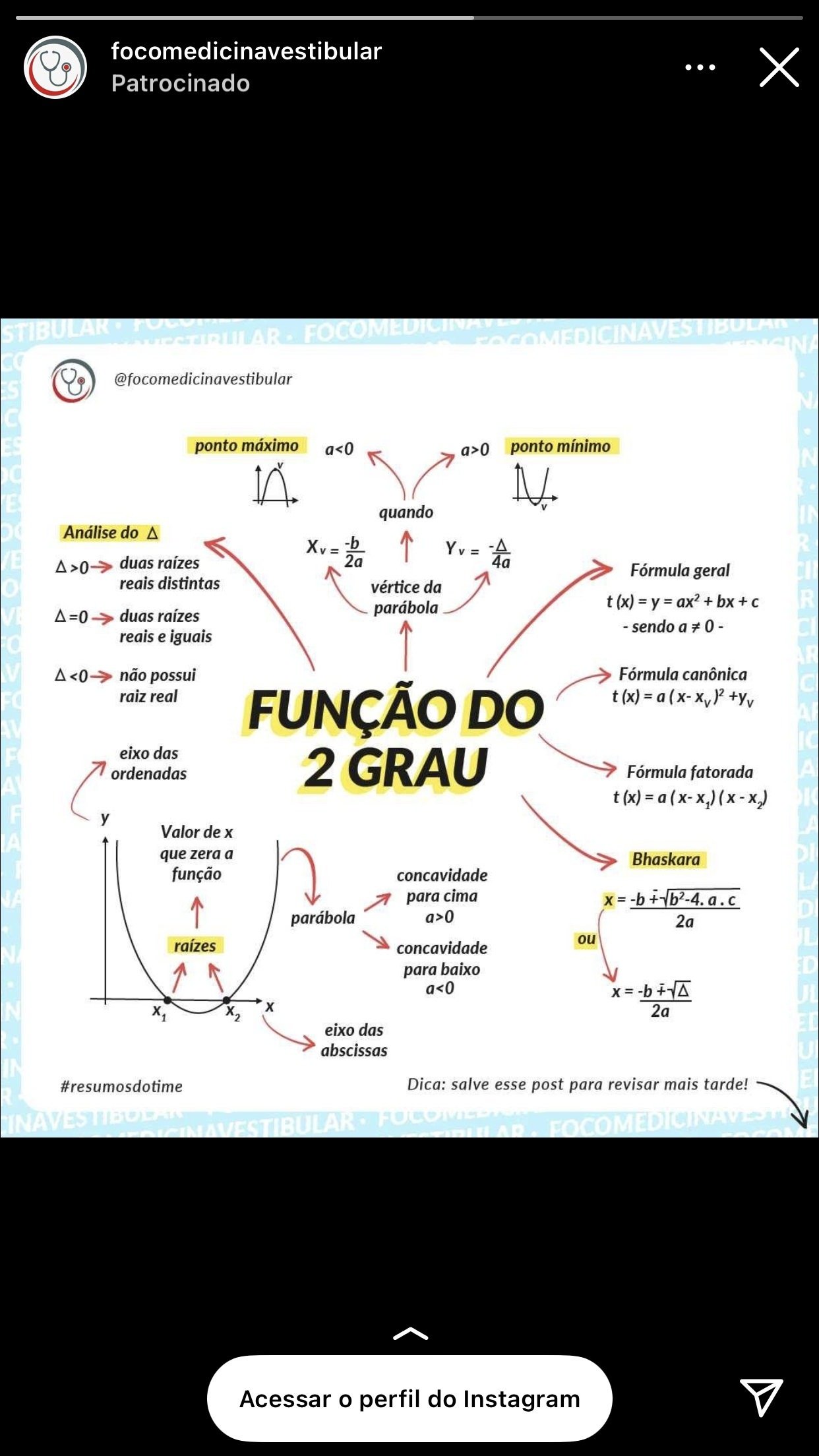
Resumo sobre Função quadrática
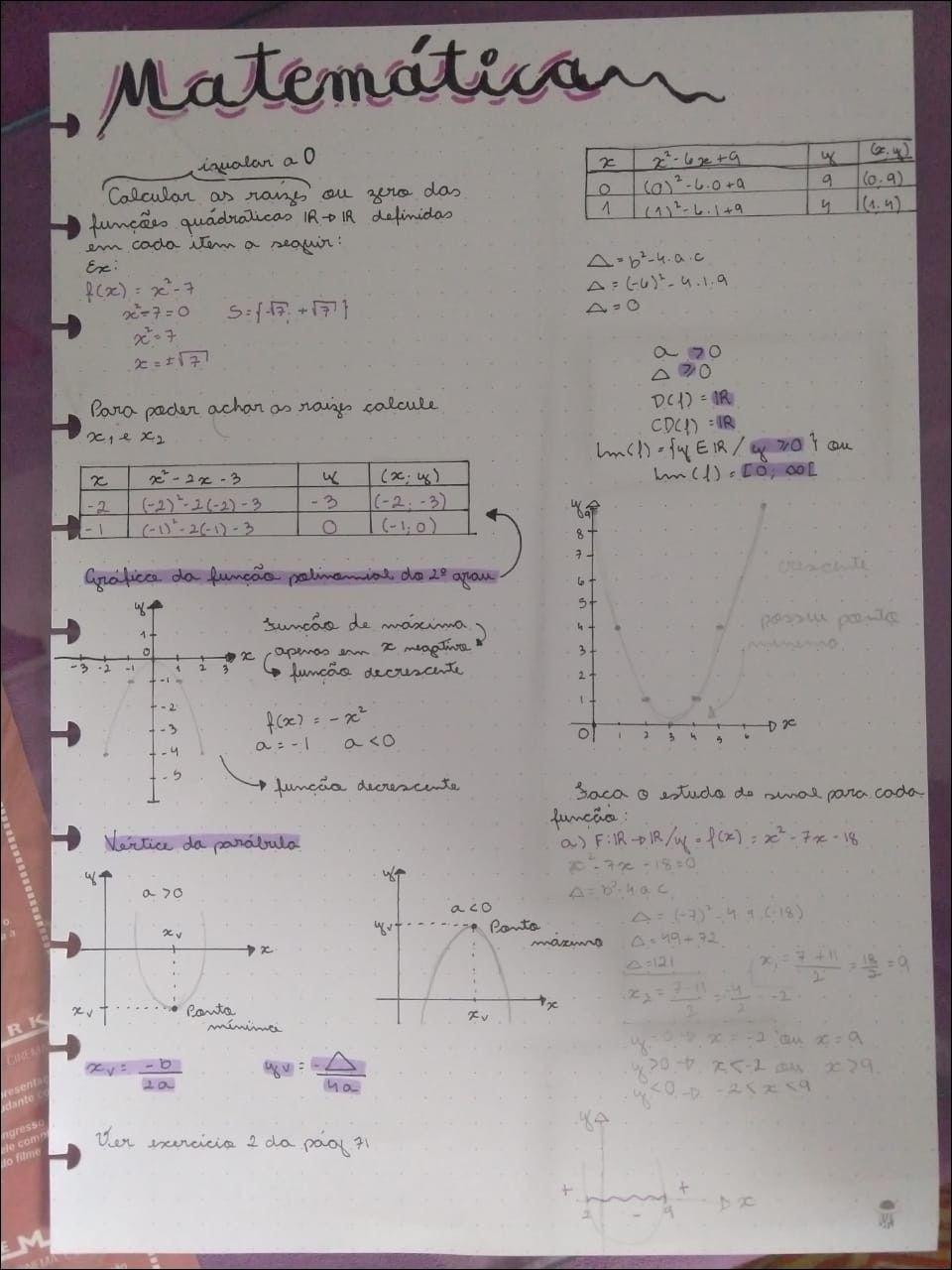
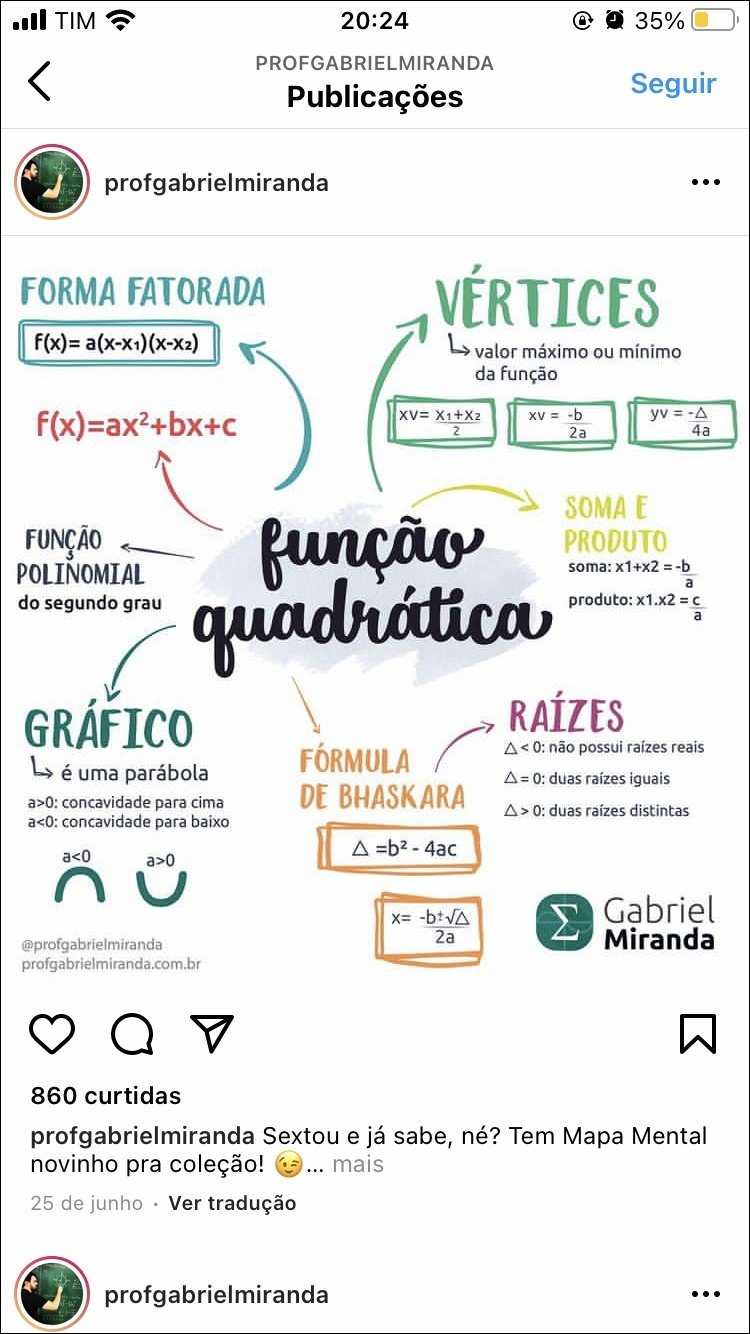
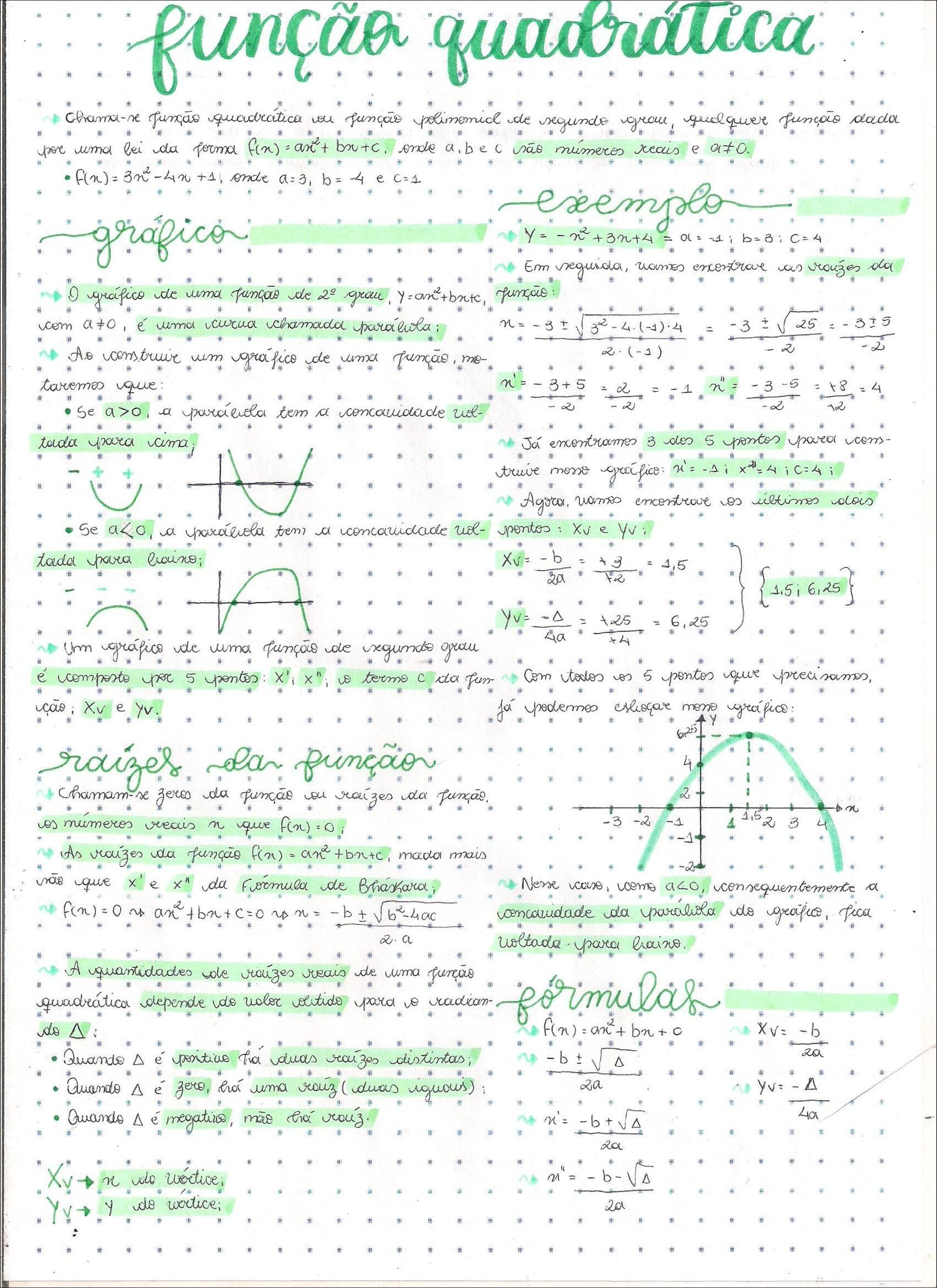
Uma função quadrática é uma função polinomial de segundo grau. Sua forma geral é dada por f(x) = ax² + bx + c, onde a, b e c são constantes reais e a ≠ 0. A representação gráfica de uma função quadrática é uma parábola.
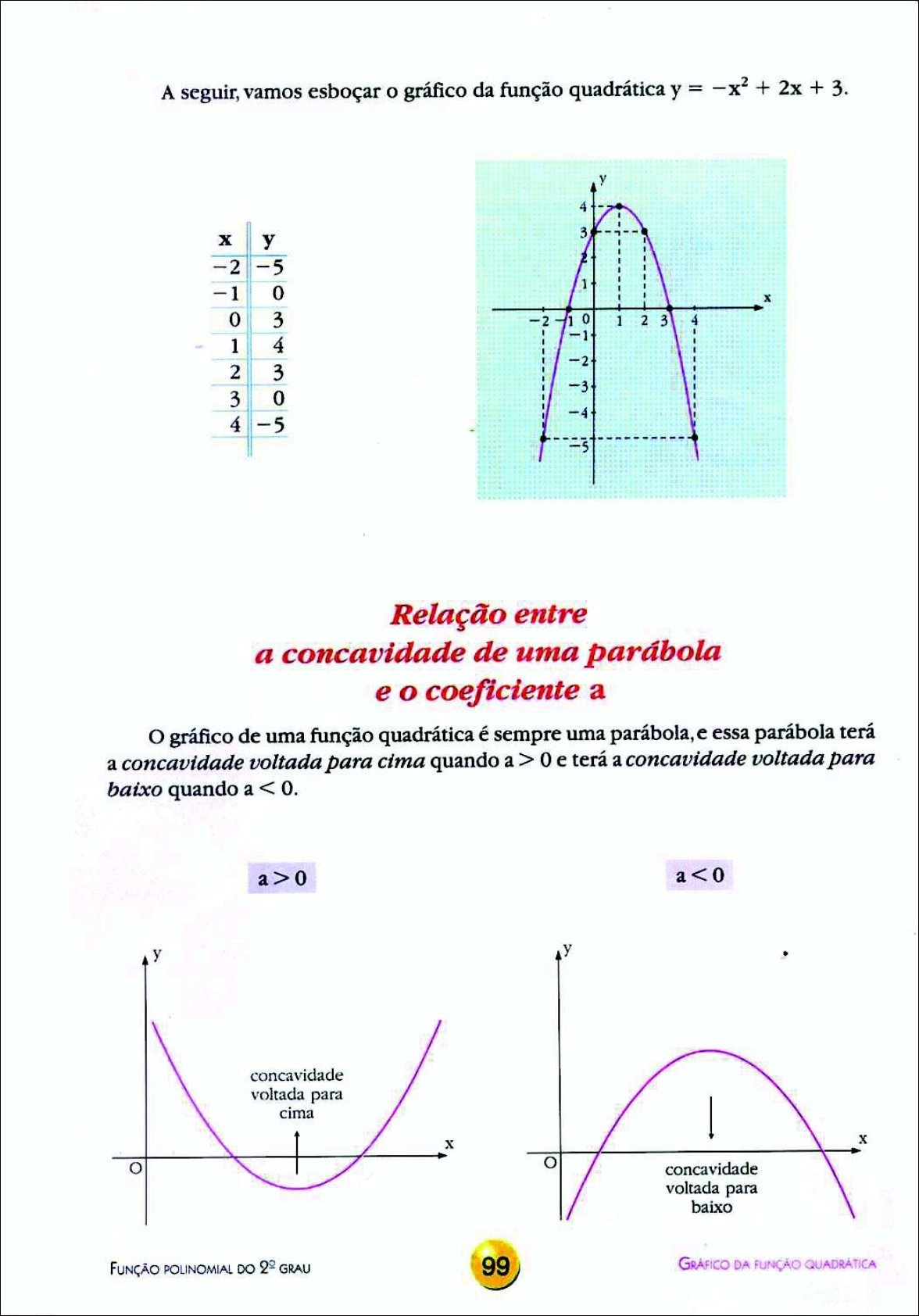
A concavidade da parábola é determinada pelo sinal de ‘a’. Se ‘a’ é positivo, a parábola abre para cima; se ‘a’ é negativo, a parábola abre para baixo. O vértice da parábola, ponto mais baixo ou mais alto da curva, representa o valor máximo ou mínimo da função. Suas coordenadas podem ser encontradas usando a fórmula do vértice: x = -b/2a. Substituindo esse valor de x na função, encontramos o valor de y correspondente.
O eixo de simetria da parábola é uma linha vertical que passa pelo vértice e divide a parábola em duas metades espelhadas. Sua equação é x = -b/2a. As raízes ou zeros da função quadrática são os valores de x para os quais f(x) = 0. Eles podem ser encontrados através da fatoração, da fórmula quadrática (-b ± √(b² – 4ac))/2a) ou analisando o gráfico.
A intersecção com o eixo y ocorre quando x = 0, o que resulta em f(0) = c. A análise da função quadrática inclui determinar concavidade, vértice, eixo de simetria, raízes, intersecção com o eixo y e o comportamento da função para valores grandes de x. A compreensão das características da função quadrática é essencial em diversas aplicações, como física (movimento de projéteis) e engenharia (design de estruturas).
