Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre relações métricas.
Mapa Mental sobre relações métricas (1)
Mapa Mental sobre relações métricas (2)

Mapa Mental sobre relações métricas (3)

Mapa Mental sobre relações métricas (4)
Mapa Mental sobre relações métricas (5)

Mapa Mental sobre relações métricas (6)
Mapa Mental sobre relações métricas (7)

Mapa Mental sobre relações métricas (8)
Mapa Mental sobre relações métricas (9)

Mapa Mental sobre relações métricas (10)

Mapa Mental sobre relações métricas (11)

Mapa Mental sobre relações métricas (12)
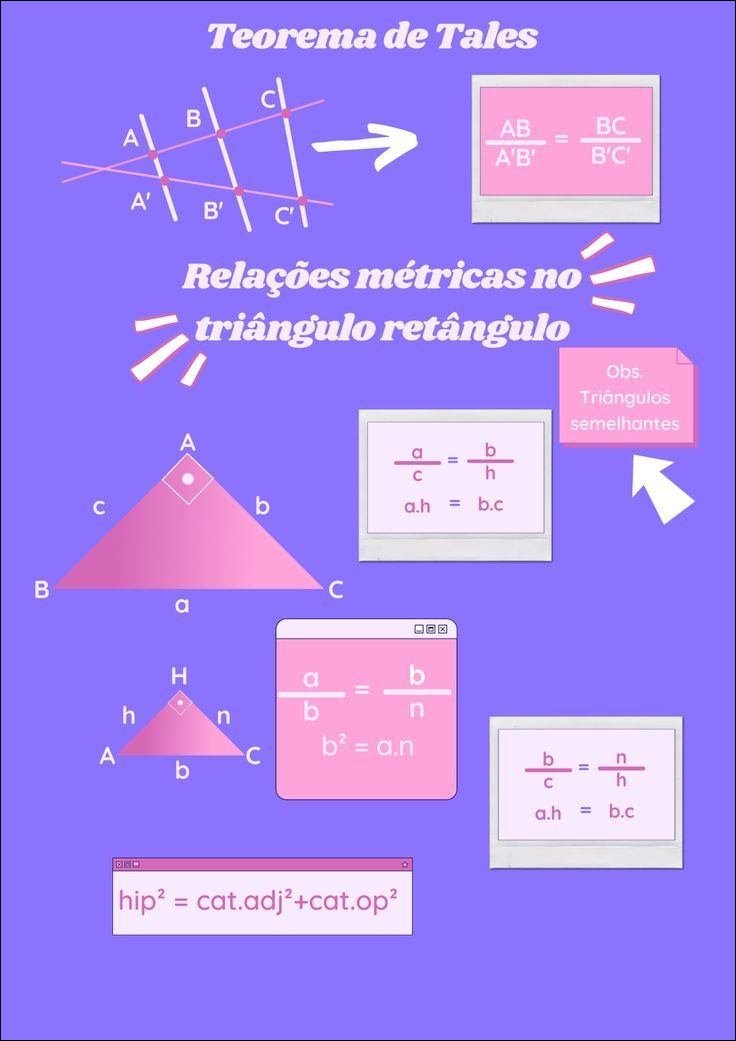
Mapa Mental sobre relações métricas (13)

Mapa Mental sobre relações métricas (14)

Mapa Mental sobre relações métricas (15)

Mapa Mental sobre relações métricas (16)
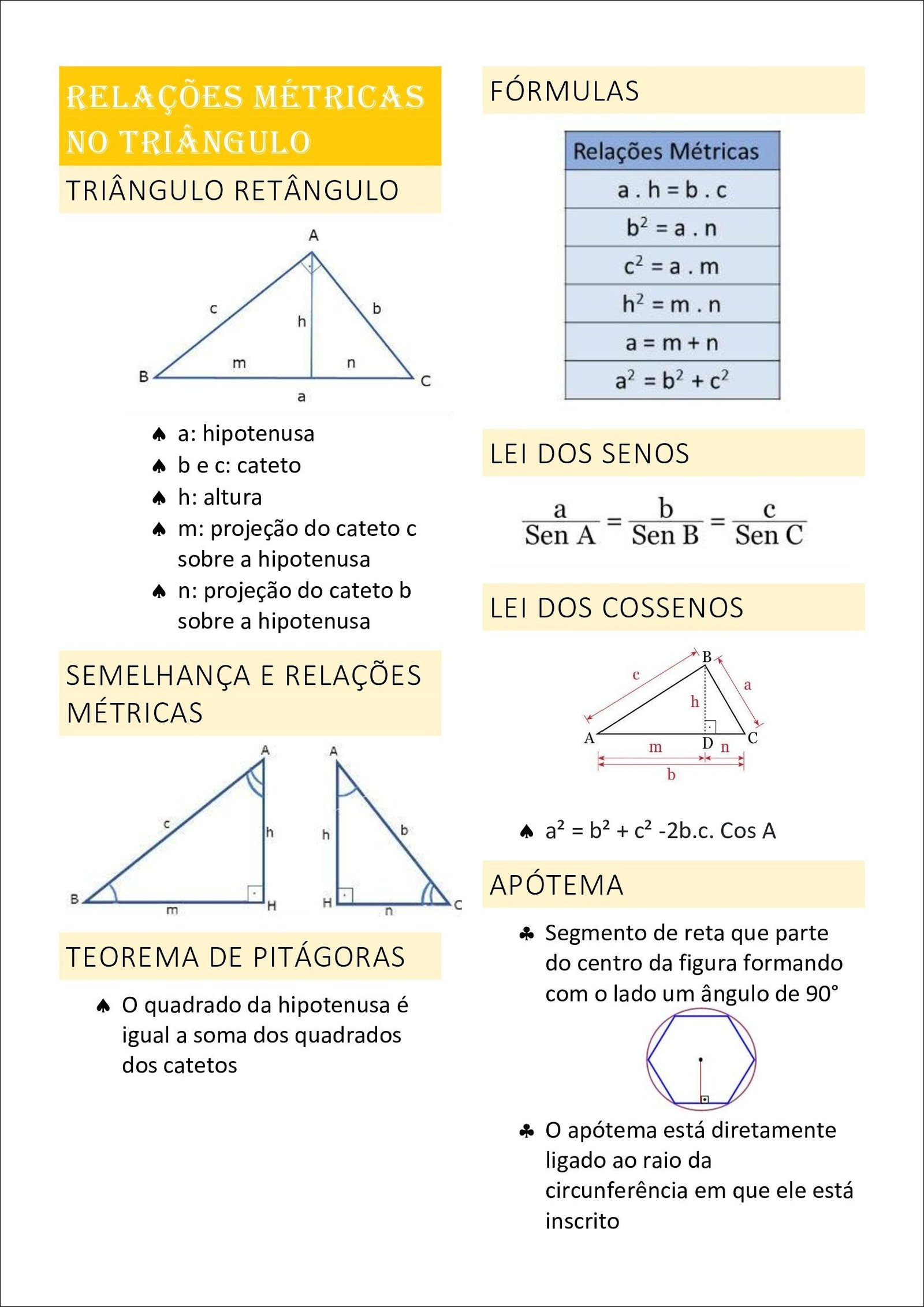
Mapa Mental sobre relações métricas (17)

Mapa Mental sobre relações métricas (18)
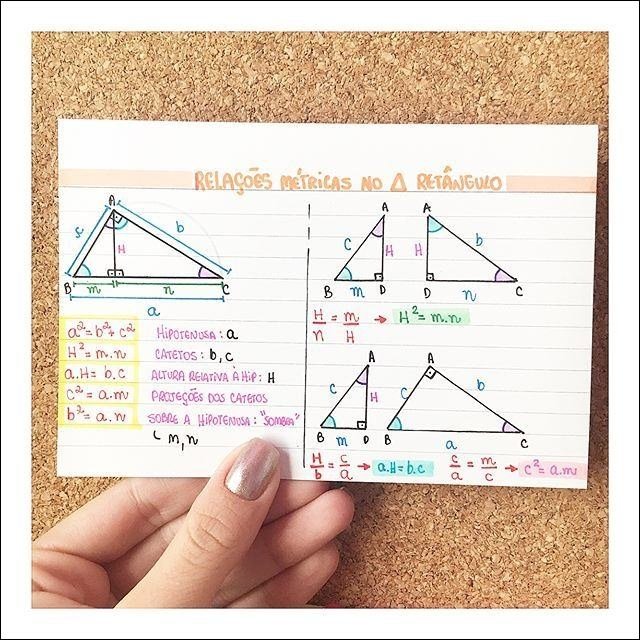
Mapa Mental sobre relações métricas (19)

Mapa Mental sobre relações métricas (20)

Resumo sobre relações métricas
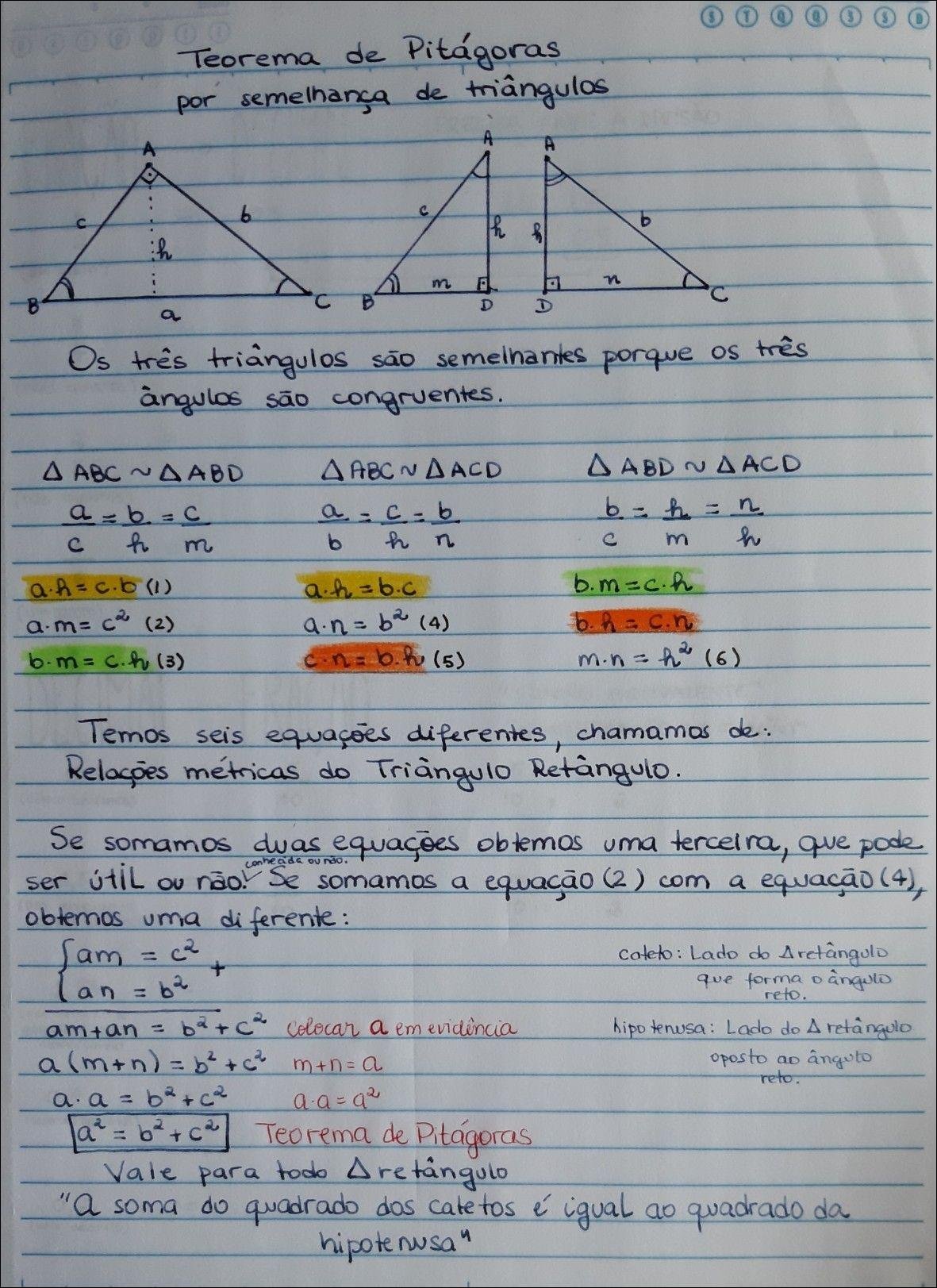
As relações métricas são um conjunto de fórmulas e teoremas que estabelecem relações entre os lados e as alturas de triângulos retângulos, bem como entre os segmentos que formam a hipotenusa quando a altura é traçada. Essas relações são cruciais para a geometria, pois permitem calcular comprimentos desconhecidos em figuras geométricas, resolver problemas de construção e entender as propriedades das formas.
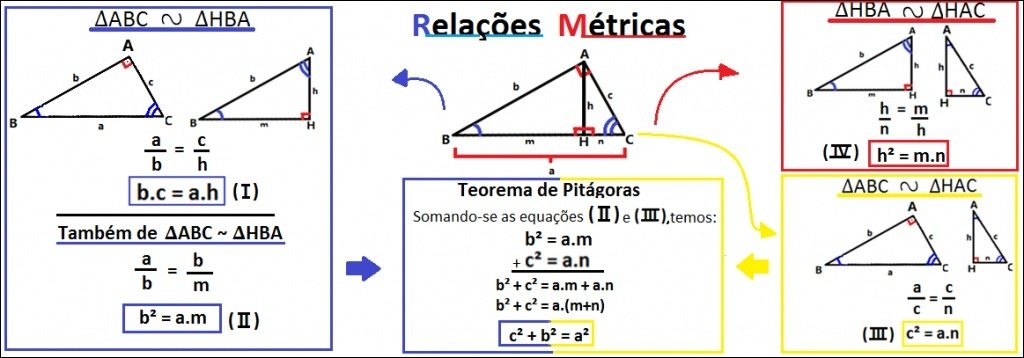
No contexto de um triângulo retângulo, a altura relativa à hipotenusa divide o triângulo em dois triângulos retângulos menores, semelhantes ao triângulo original. As relações métricas derivam dessas semelhanças e estabelecem igualdades como: a² = m.n, b² = m.n, h² = m.n, onde a e b são os catetos, h é a altura, m e n são as projeções dos catetos na hipotenusa, e a é a hipotenusa.
Além disso, o Teorema de Pitágoras (a² + b² = c²) é uma relação métrica fundamental, conectando os comprimentos dos lados de um triângulo retângulo.
As relações métricas são amplamente utilizadas em diversas áreas, como engenharia, arquitetura e design, para calcular distâncias, ângulos e áreas, além de servirem como base para a compreensão de conceitos geométricos mais complexos. O domínio dessas relações é essencial para a resolução de problemas práticos e o desenvolvimento de habilidades de raciocínio geométrico.
