Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre função de 2º grau.
Mapa Mental sobre função de 2º grau (1)

Mapa Mental sobre função de 2º grau (2)
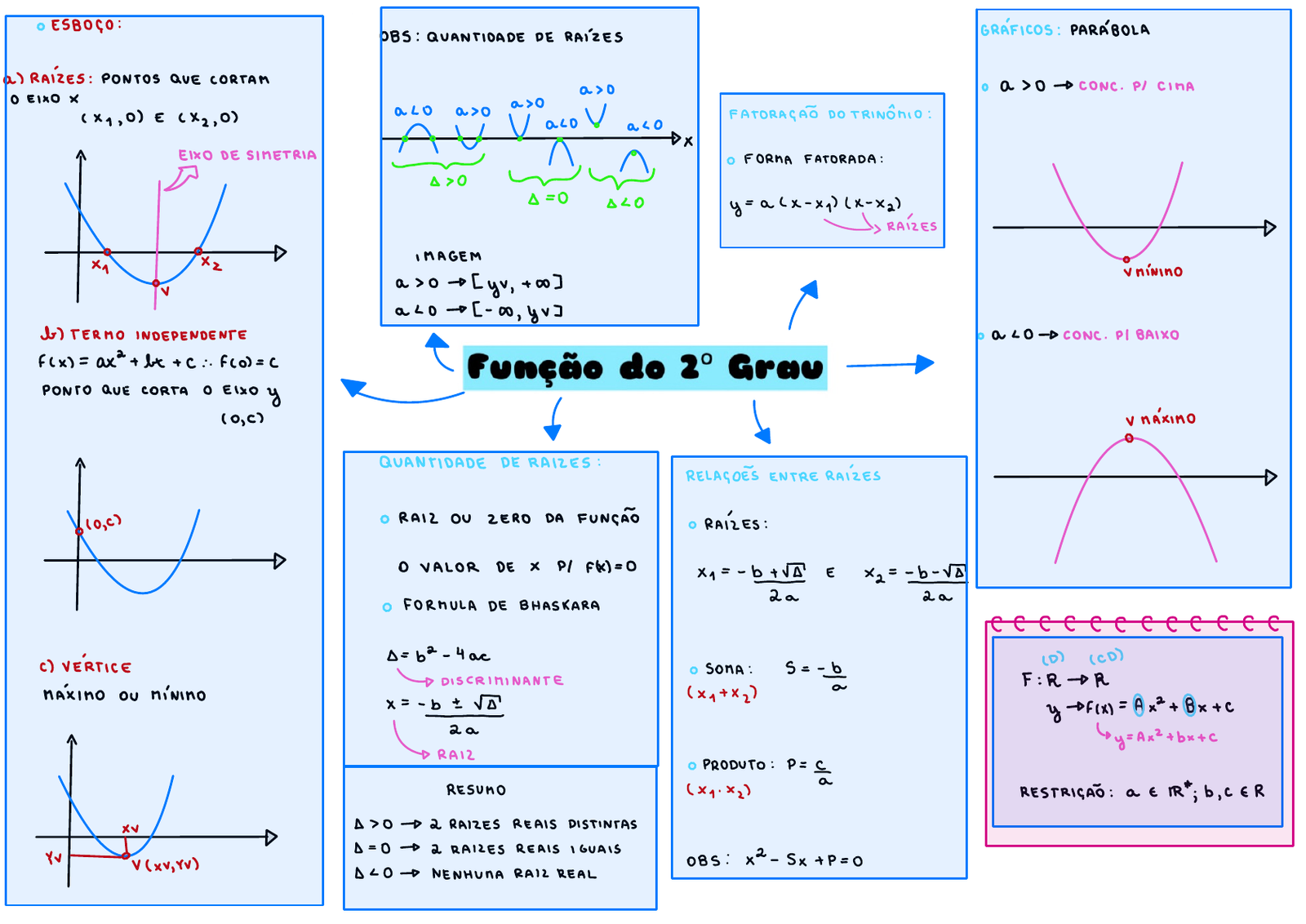
Mapa Mental sobre função de 2º grau (3)
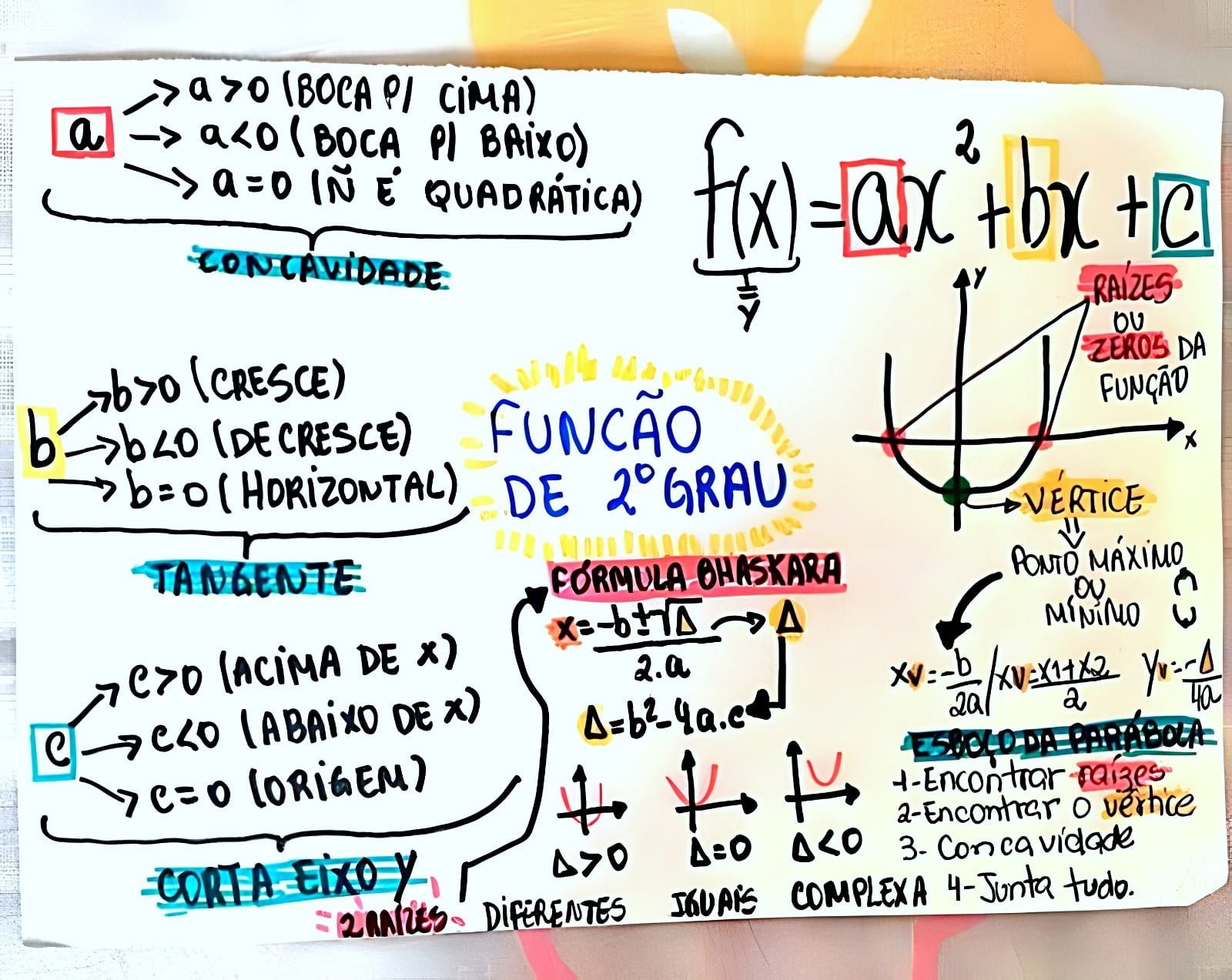
Mapa Mental sobre função de 2º grau (4)

Mapa Mental sobre função de 2º grau (5)
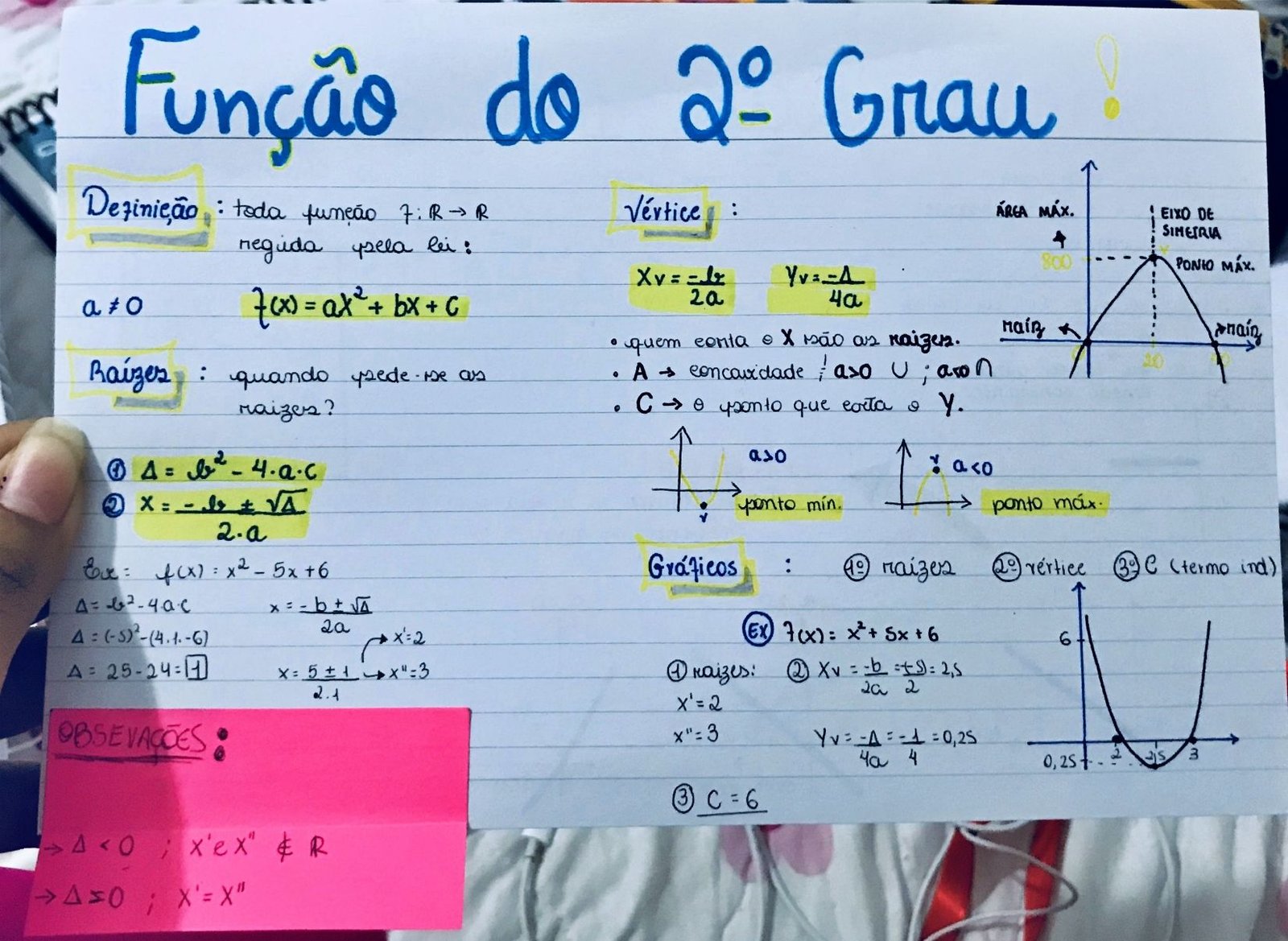
Mapa Mental sobre função de 2º grau (6)

Mapa Mental sobre função de 2º grau (7)
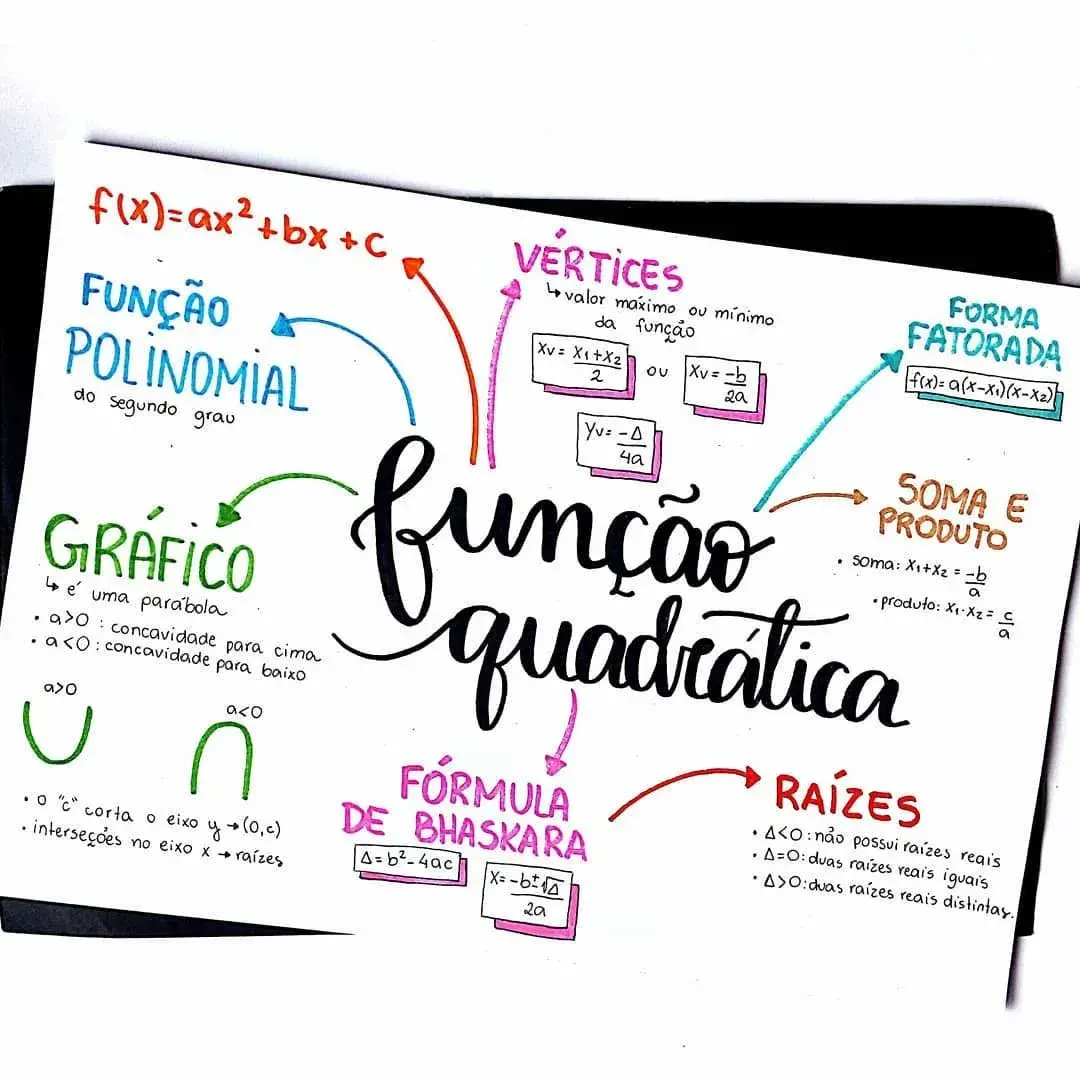
Mapa Mental sobre função de 2º grau (8)

Mapa Mental sobre função de 2º grau (9)
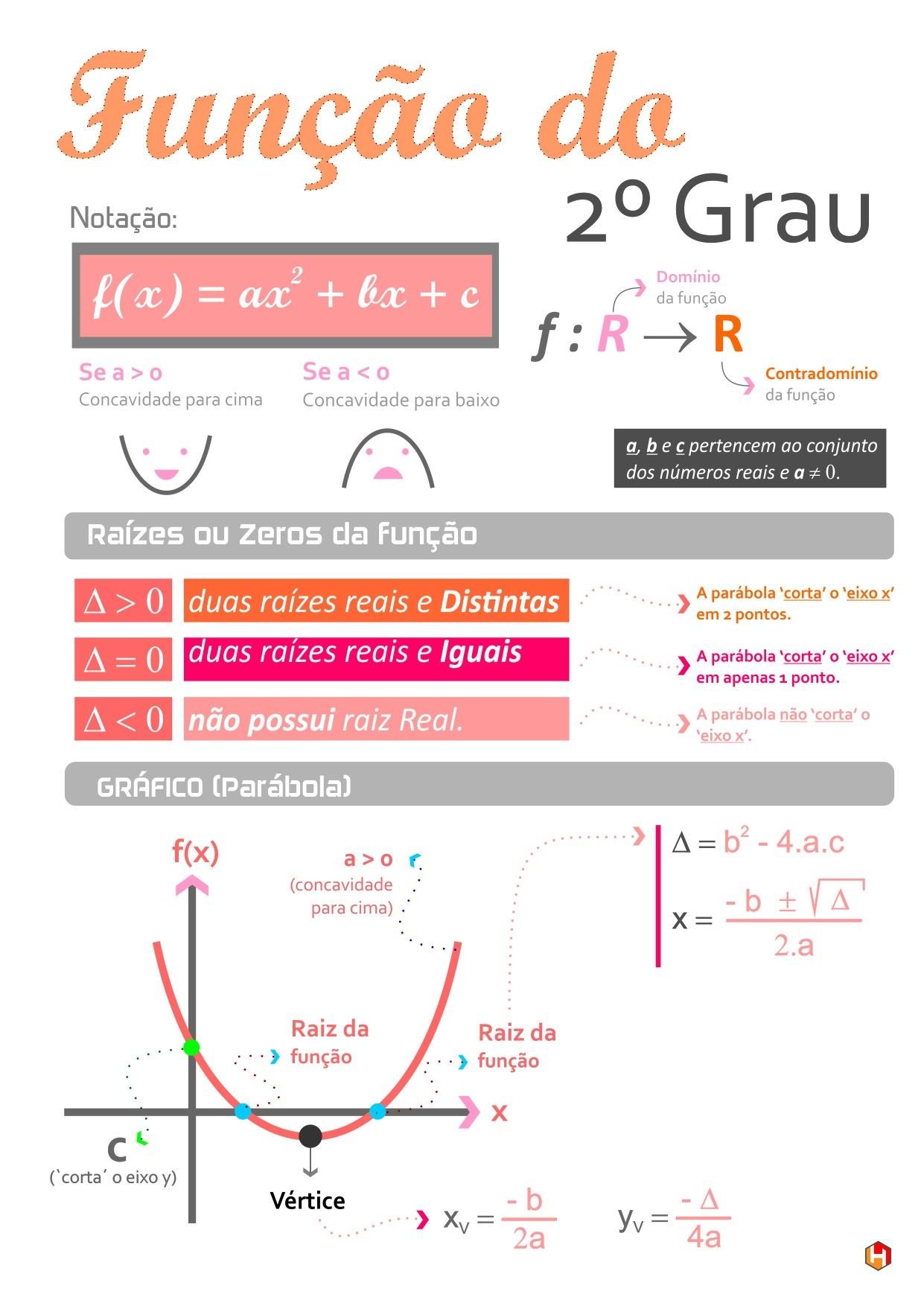
Mapa Mental sobre função de 2º grau (10)

Resumo sobre função de 2º grau
A função de segundo grau, também conhecida como função quadrática, é uma função polinomial definida pela equação geral f(x) = ax² + bx + c, onde ‘a’, ‘b’ e ‘c’ são números reais e ‘a’ é diferente de zero. Ela descreve uma parábola, uma curva em forma de U, que pode ser voltada para cima (quando a > 0) ou para baixo (quando a < 0).
A análise da função de segundo grau envolve a determinação de suas principais características. O vértice da parábola, ponto de máximo ou mínimo da função, é crucial e pode ser calculado usando as fórmulas V(x) = -b/2a e V(y) = -Δ/4a, onde Δ (delta) = b² – 4ac. O valor de Δ revela a natureza das raízes (pontos onde a parábola intersecta o eixo x): Δ > 0 indica duas raízes reais e distintas; Δ = 0 indica uma raiz real (uma única interseção com o eixo x); e Δ < 0 indica que não há raízes reais (a parábola não toca o eixo x).
A concavidade da parábola é determinada pelo valor de ‘a’. Se ‘a’ é positivo, a parábola tem concavidade voltada para cima e o vértice representa o ponto de mínimo. Se ‘a’ é negativo, a concavidade é voltada para baixo e o vértice representa o ponto de máximo.
Entender a função de segundo grau é essencial em diversas áreas da matemática e ciências, como física (para descrever a trajetória de projéteis), economia (para modelar custos e receitas) e engenharia. A capacidade de analisar e interpretar os parâmetros ‘a’, ‘b’ e ‘c’, identificar o vértice, as raízes e a concavidade permite uma compreensão profunda do comportamento da função e sua aplicação em problemas práticos.
