Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre Números complexos.
Mapa Mental sobre Números complexos (1)

Mapa Mental sobre Números complexos (2)

Mapa Mental sobre Números complexos (3)
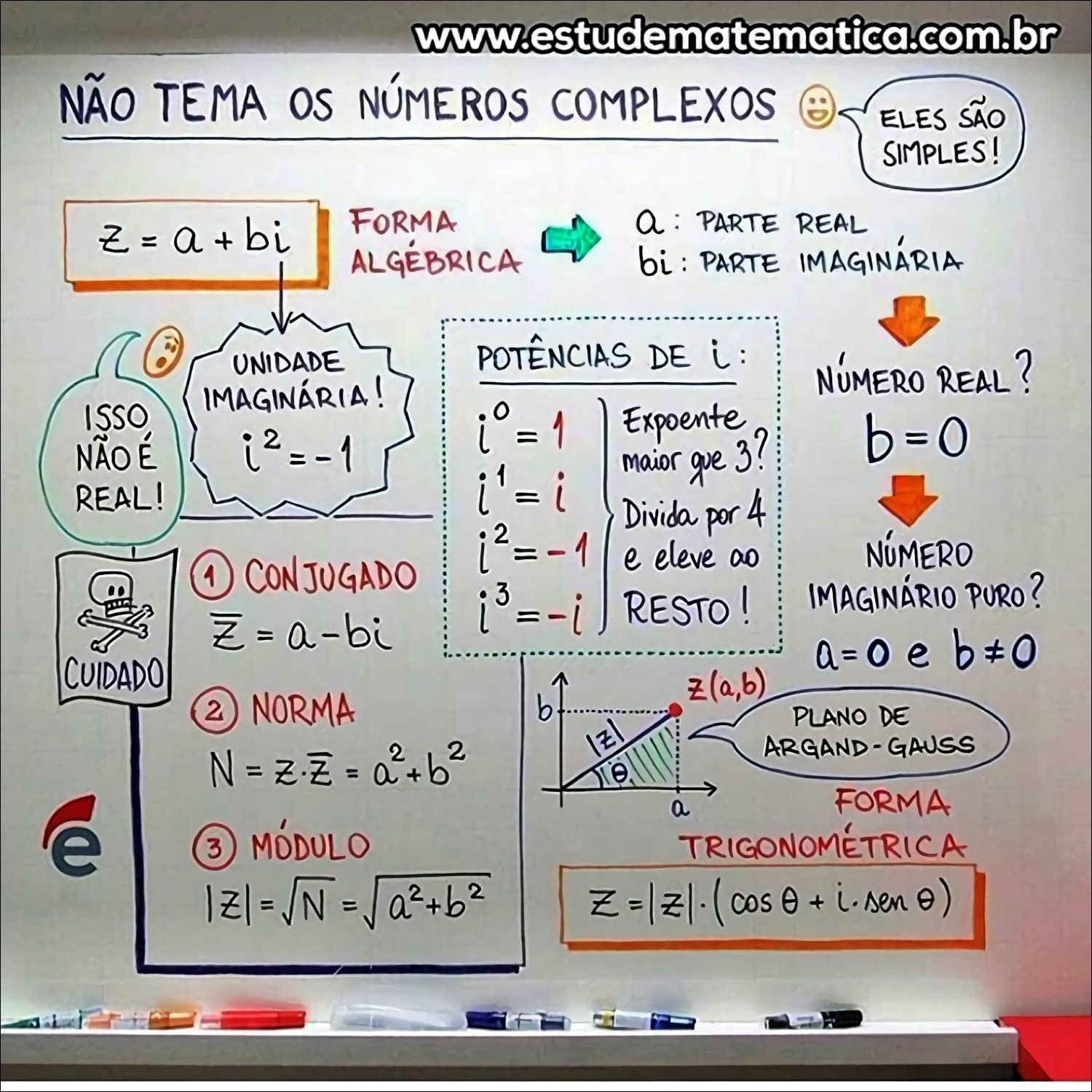
Mapa Mental sobre Números complexos (4)

Mapa Mental sobre Números complexos (5)

Mapa Mental sobre Números complexos (6)

Mapa Mental sobre Números complexos (7)

Mapa Mental sobre Números complexos (8)
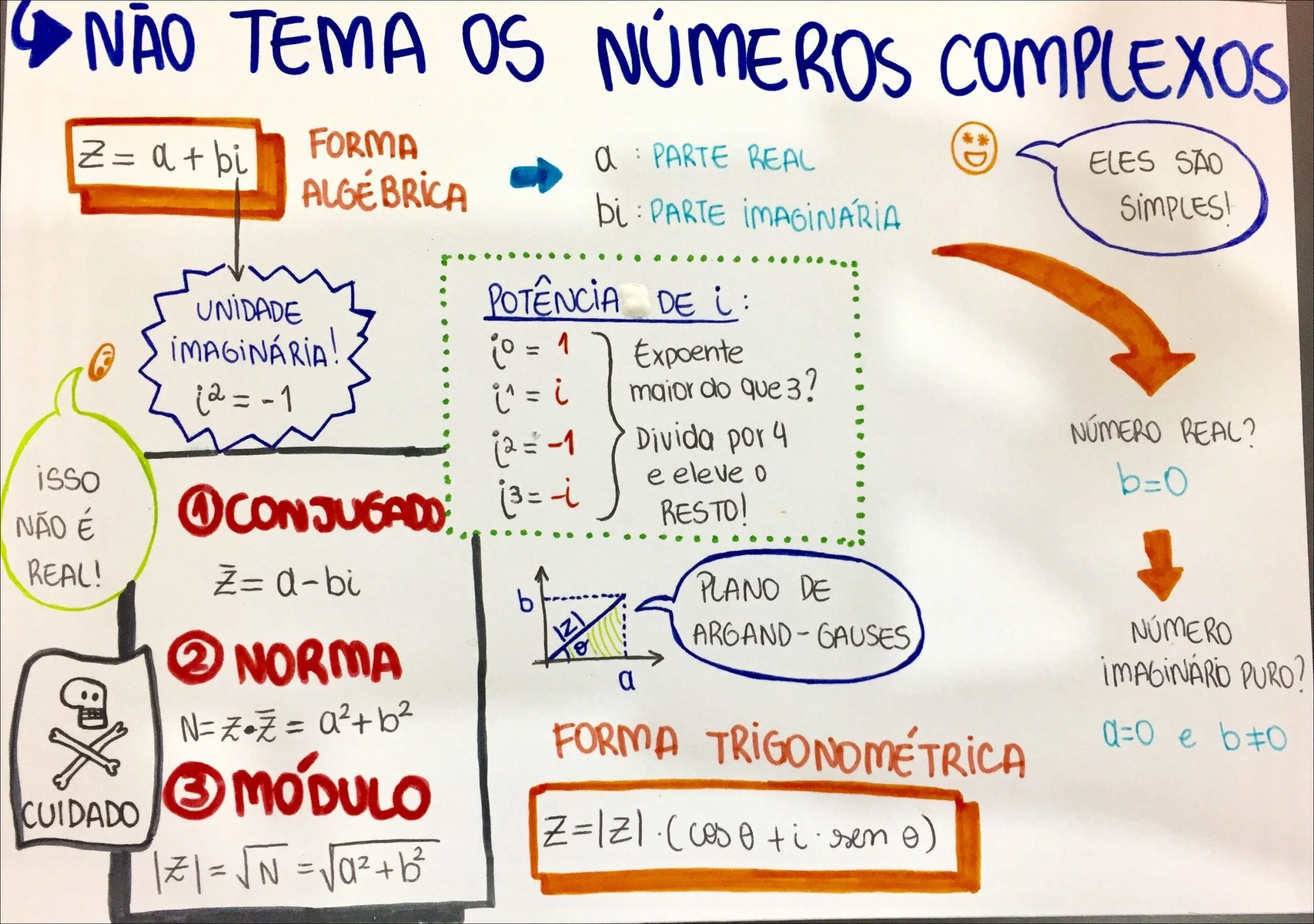
Mapa Mental sobre Números complexos (9)

Mapa Mental sobre Números complexos (10)

Mapa Mental sobre Números complexos (11)

Mapa Mental sobre Números complexos (12)

Mapa Mental sobre Números complexos (13)

Mapa Mental sobre Números complexos (14)

Mapa Mental sobre Números complexos (15)

Mapa Mental sobre Números complexos (16)
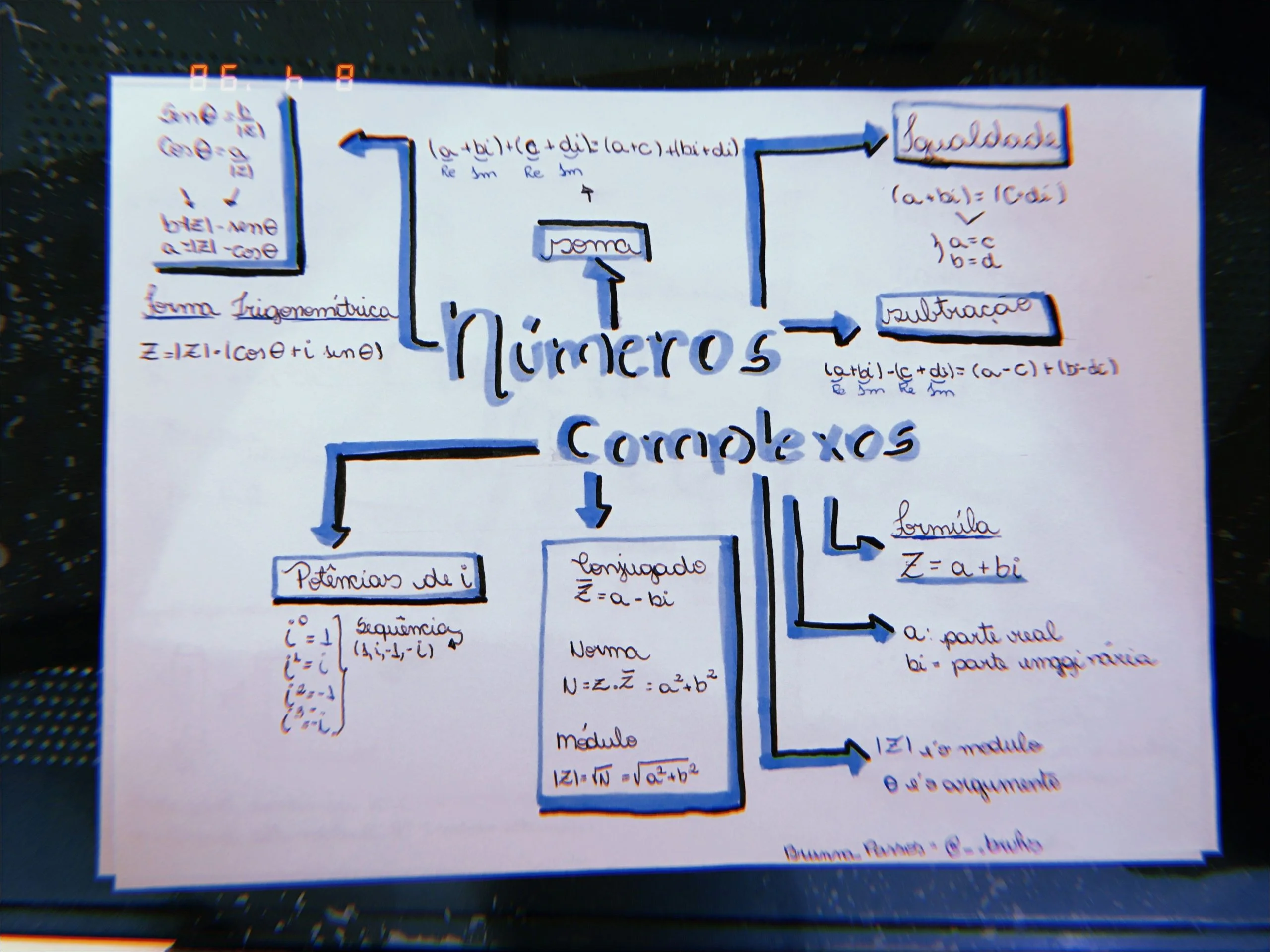
Mapa Mental sobre Números complexos (17)

Mapa Mental sobre Números complexos (18)
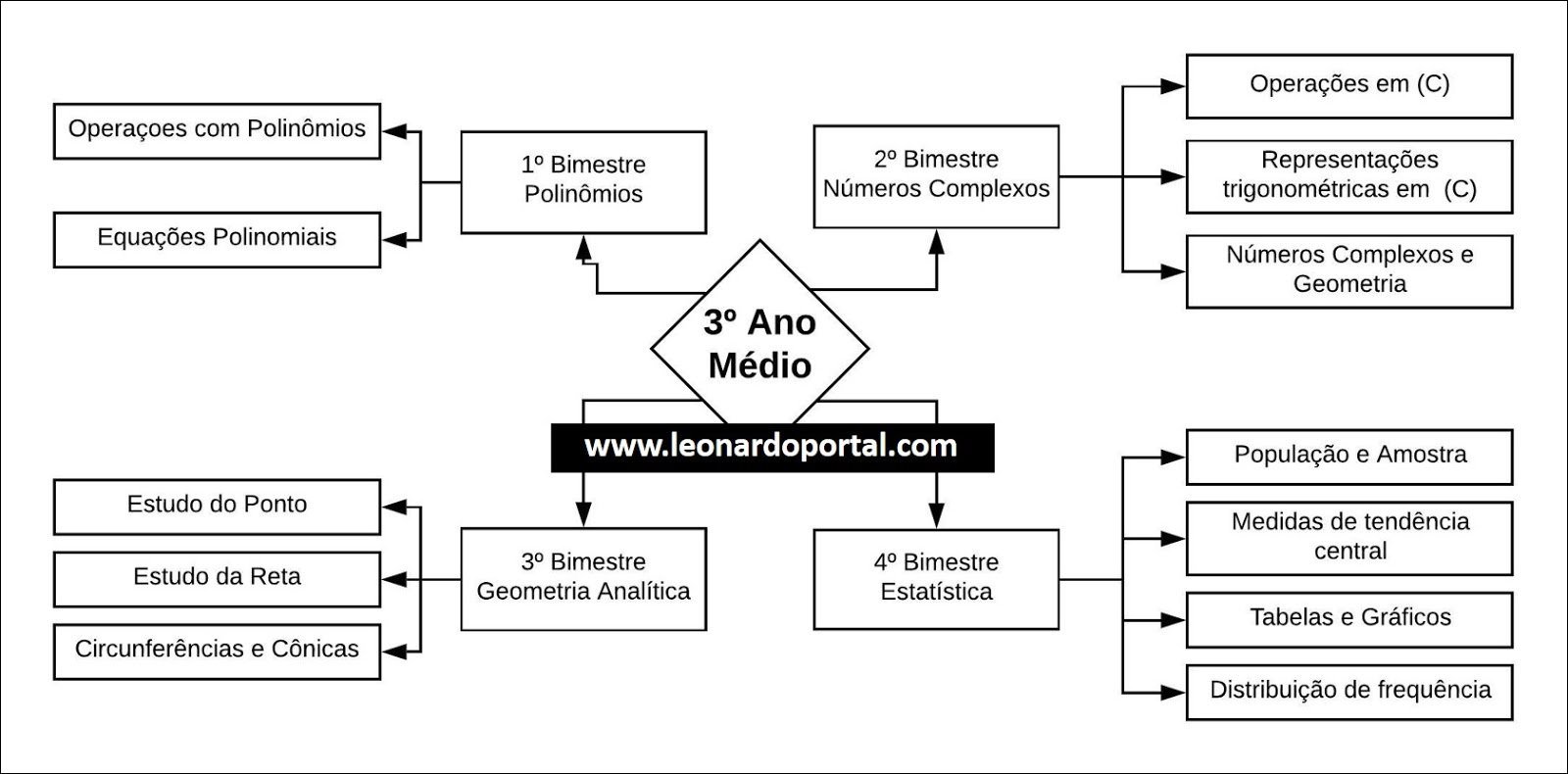
Mapa Mental sobre Números complexos (19)

Mapa Mental sobre Números complexos (20)
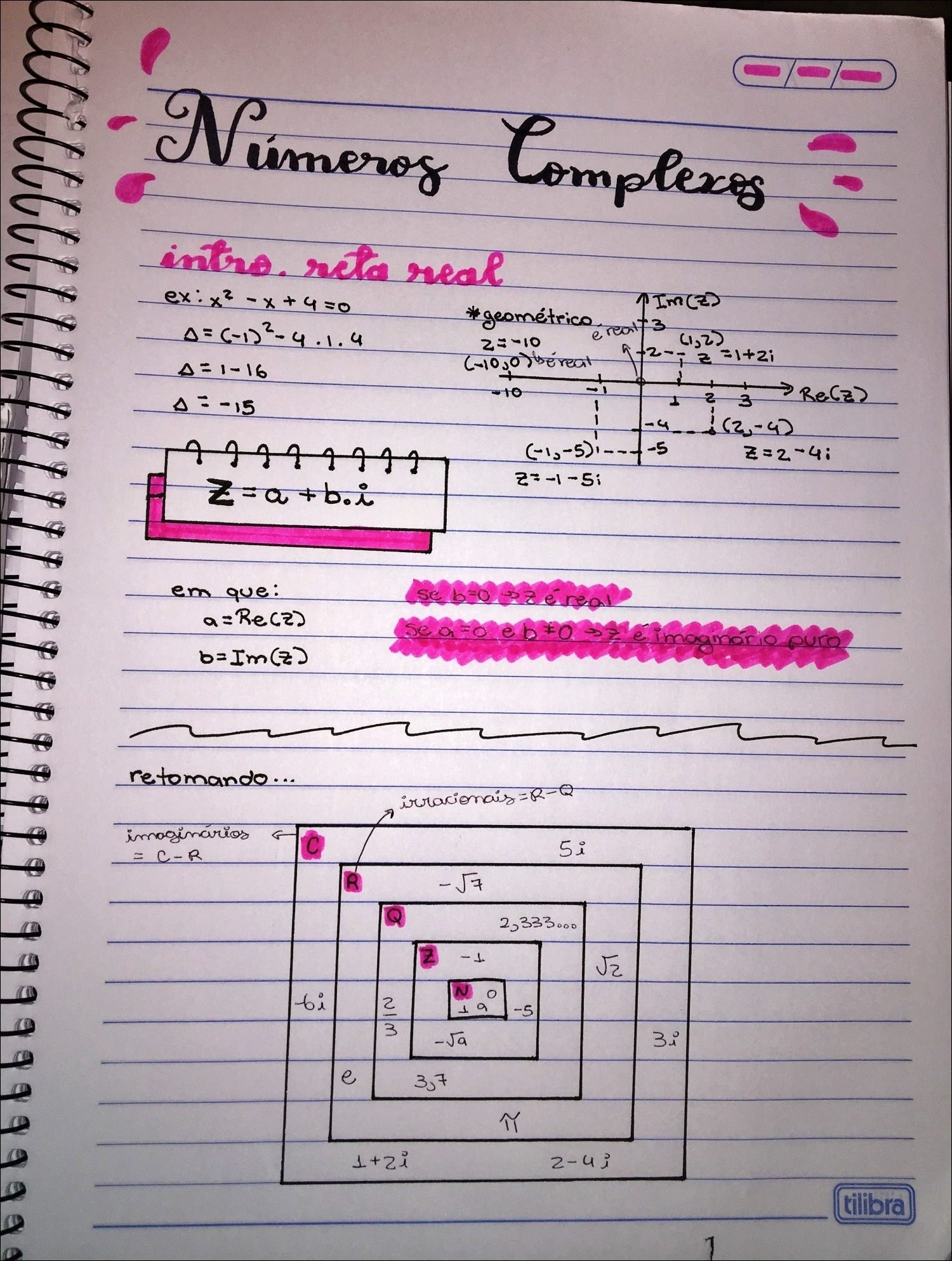
Mapa Mental sobre Números complexos (21)

Resumo sobre Números complexos
Números complexos são números que podem ser expressos na forma a + bi, onde a e b são números reais e i é a unidade imaginária, definida como a raiz quadrada de -1. Eles surgiram pela primeira vez como uma ferramenta para resolver equações polinomiais que não tinham soluções reais.
Os números complexos formam um campo chamado plano complexo, onde o eixo real representa números reais e o eixo imaginário representa números imaginários. Distâncias no plano complexo são medidas usando o módulo, que é a distância de um número complexo até a origem. O argumento de um número complexo é o ângulo entre o eixo real e o vetor que liga o número à origem.
Operações aritméticas em números complexos são realizadas como se a e b fossem independentes: adição, subtração, multiplicação e divisão. A multiplicação é particularmente importante, pois ela envolve o uso da identidade i² = -1.
Números complexos têm muitas aplicações em ciência, engenharia e matemática. Eles são usados em análise de circuitos elétricos, mecânica quântica e outros campos onde quantidades físicas têm magnitude e direção. Além disso, eles são essenciais para o estudo de funções holomorfas, que são funções que são diferenciáveis em todos os pontos do plano complexo.
