Compilação com os melhores mapas mentais, conceituais, infográficos, diagramas e resumos sobre poliedros.
Mapa Mental sobre poliedros (1)
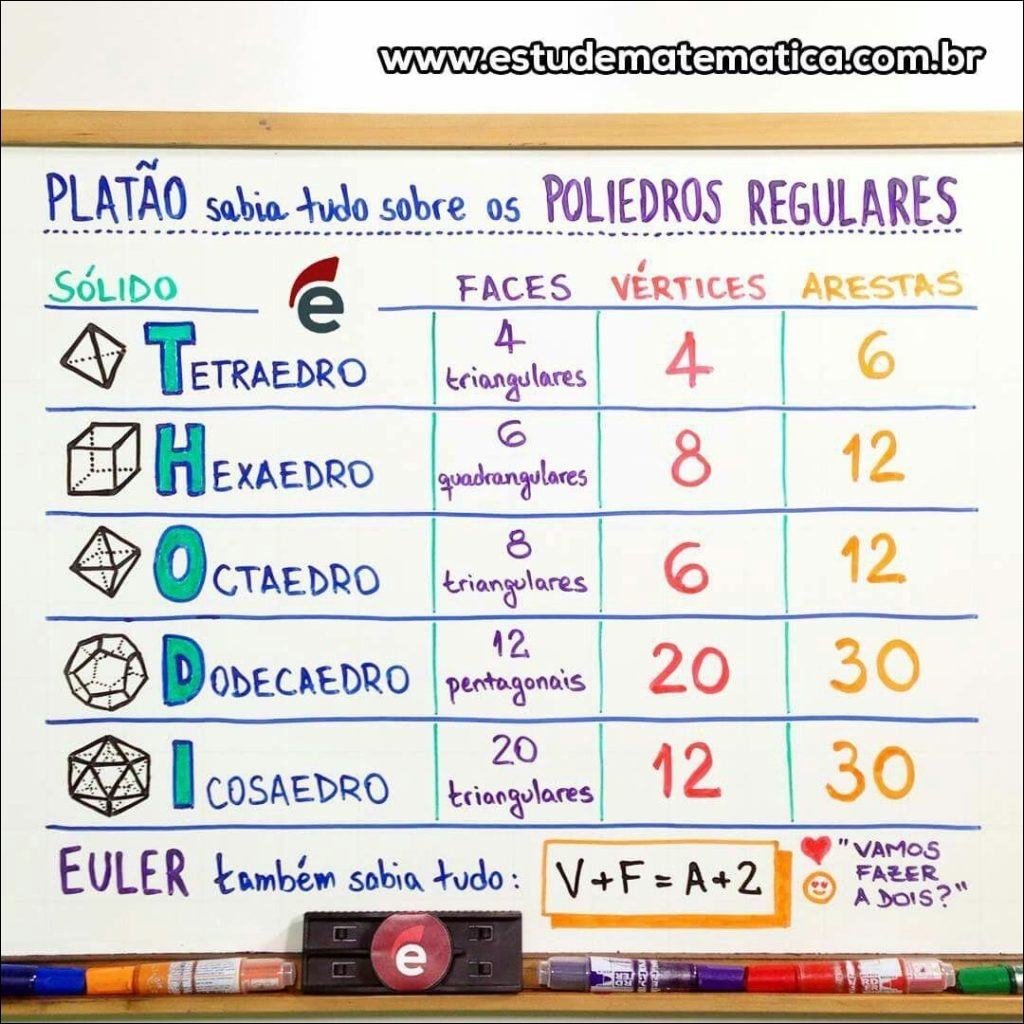
Mapa Mental sobre poliedros (2)

Mapa Mental sobre poliedros (3)
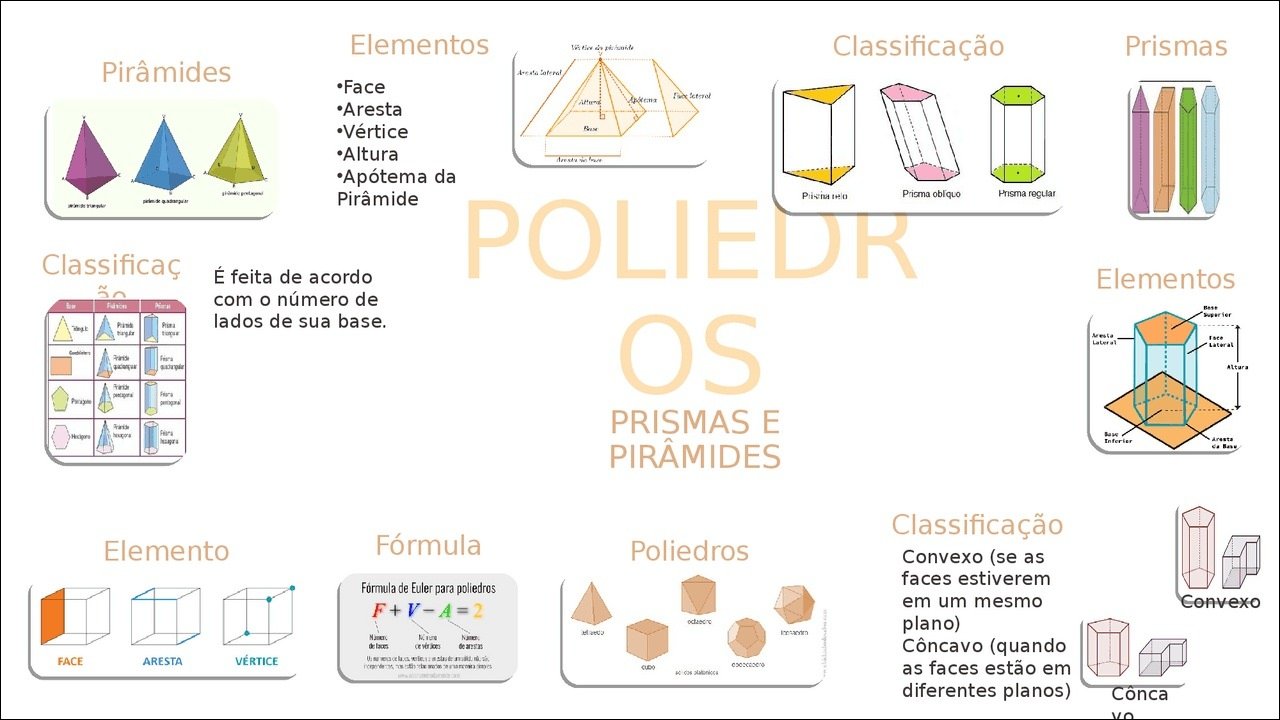
Mapa Mental sobre poliedros (4)
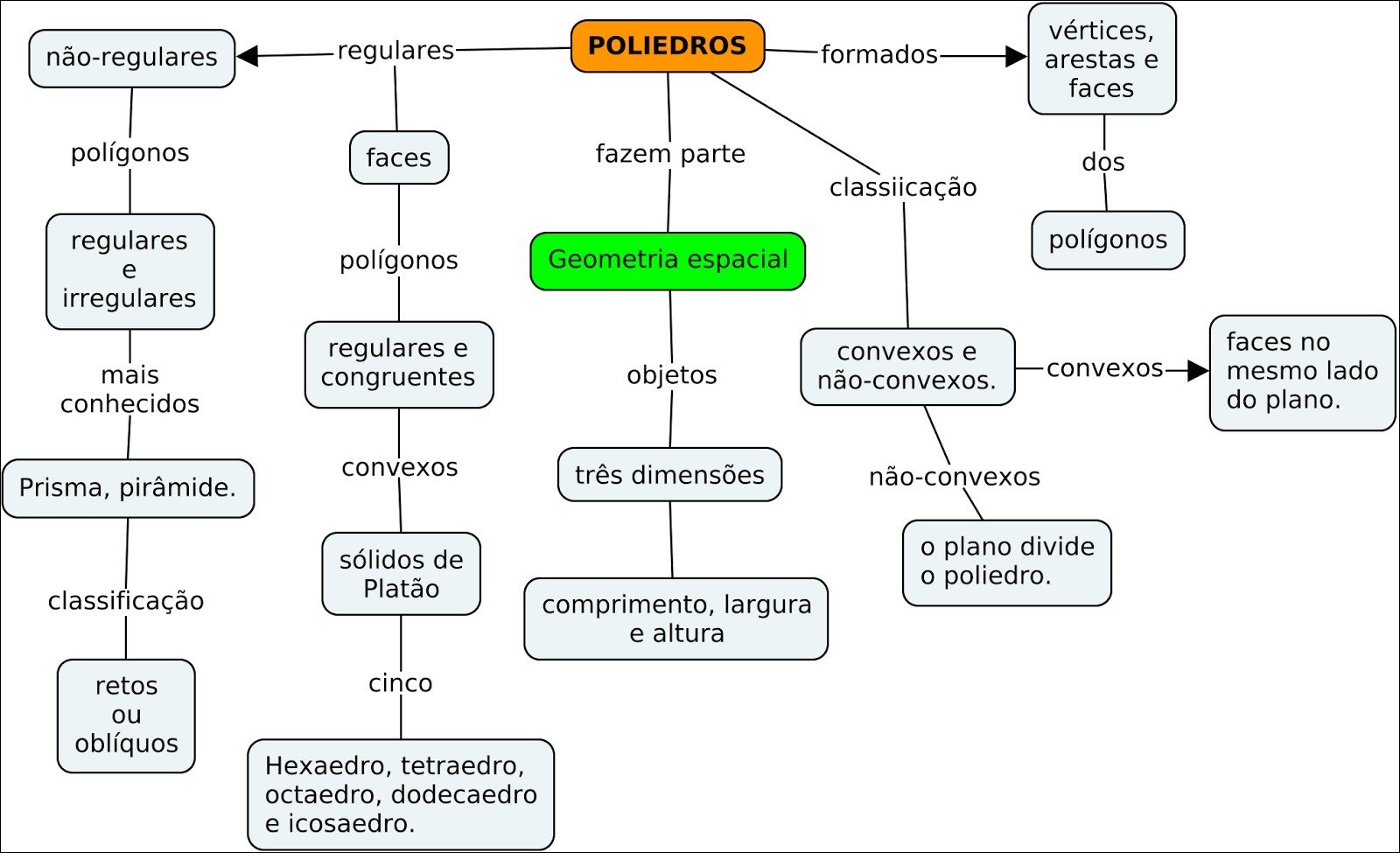
Mapa Mental sobre poliedros (5)
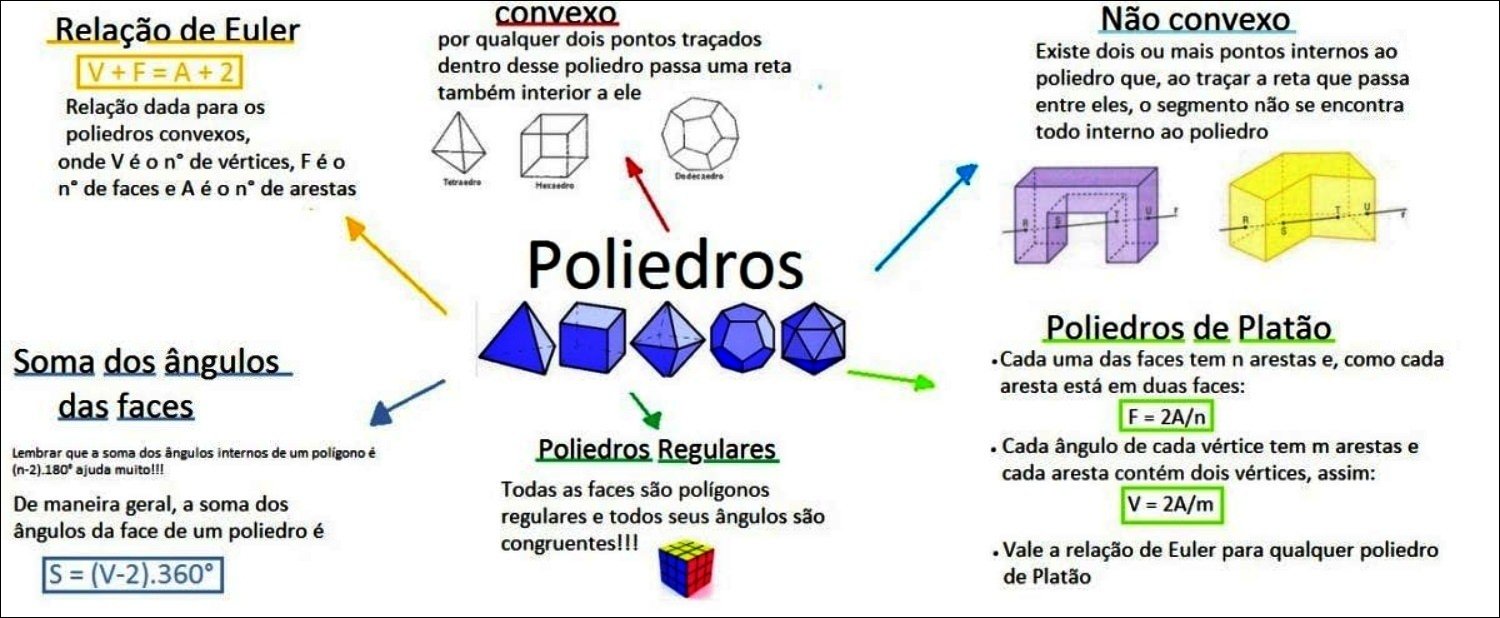
Mapa Mental sobre poliedros (6)

Mapa Mental sobre poliedros (7)

Mapa Mental sobre poliedros (8)
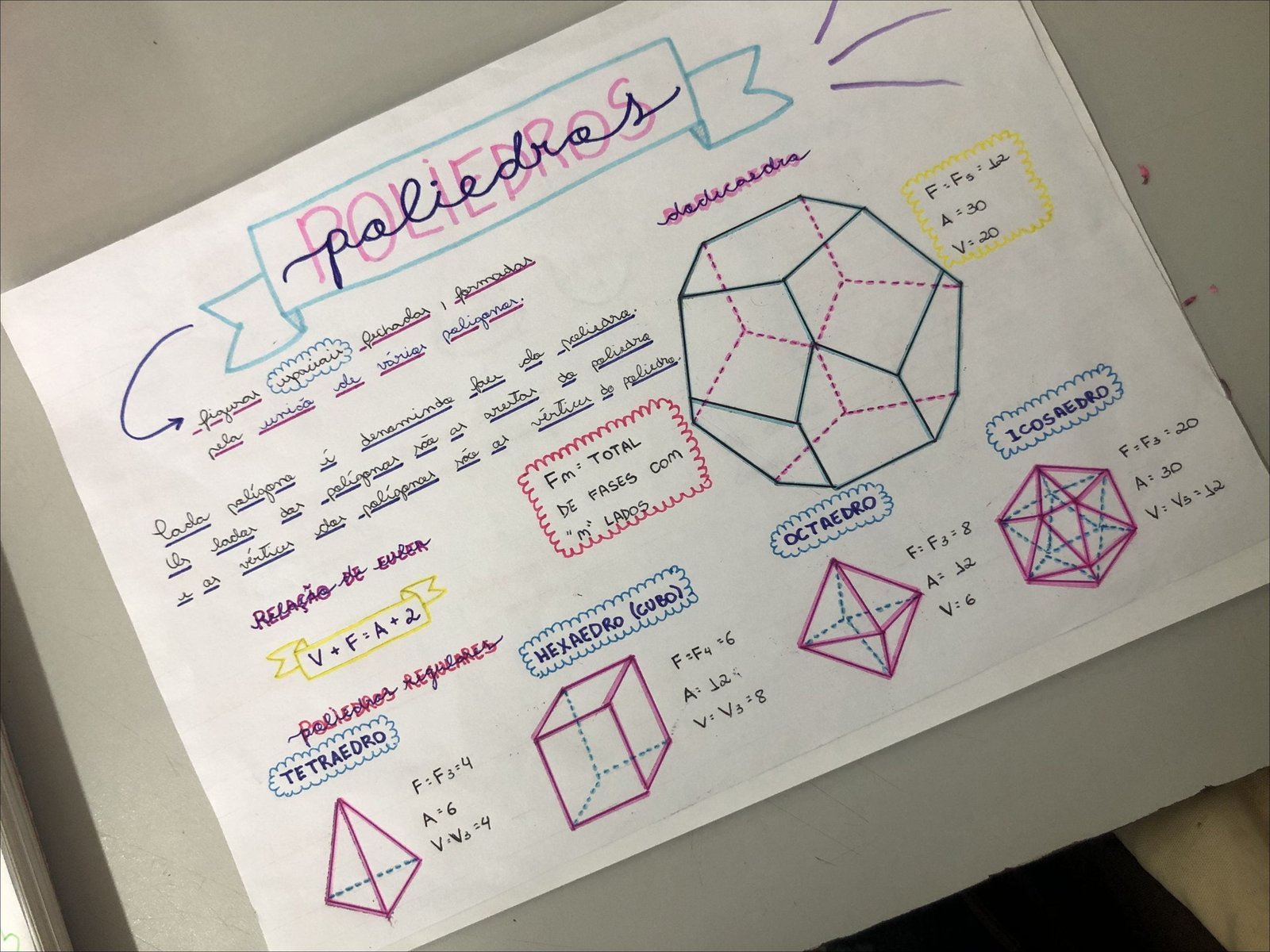
Mapa Mental sobre poliedros (9)
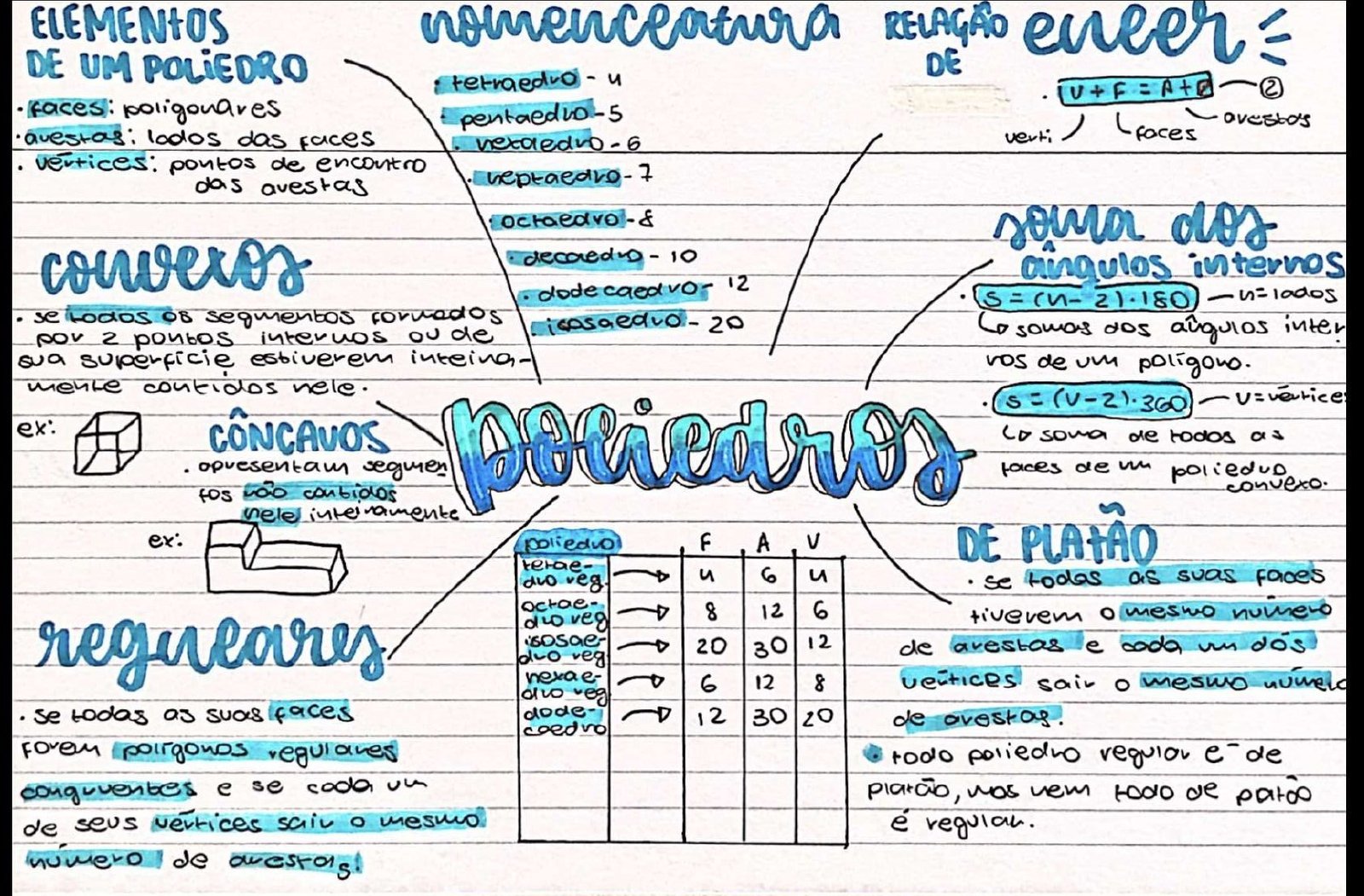
Mapa Mental sobre poliedros (10)
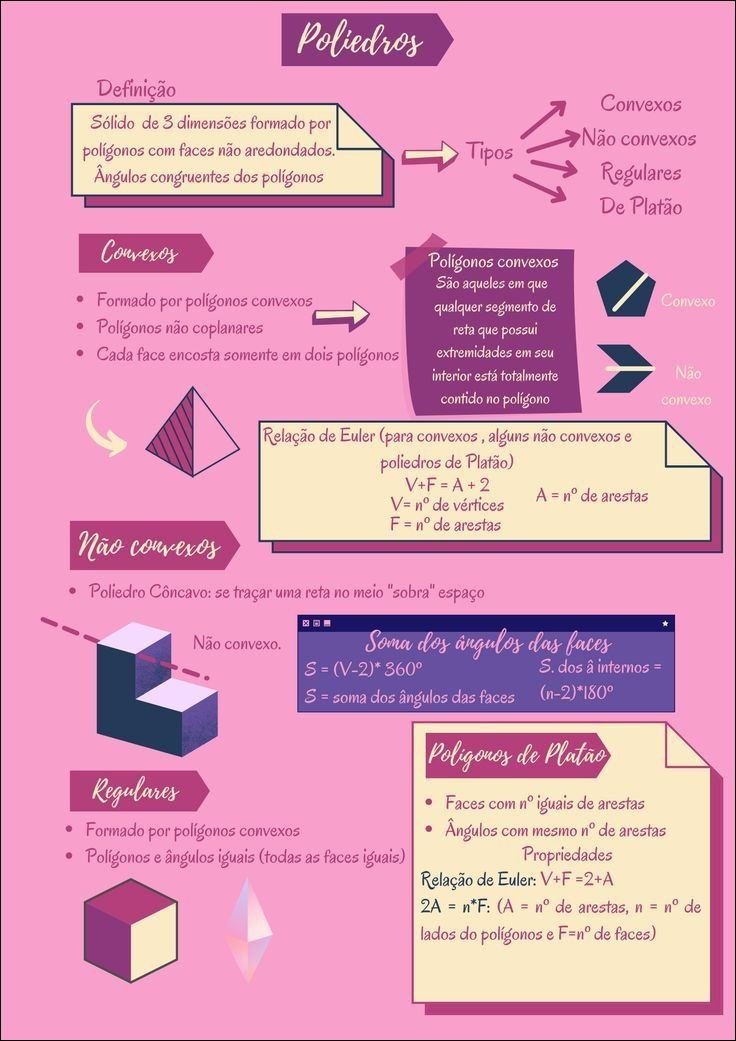
Mapa Mental sobre poliedros (11)

Mapa Mental sobre poliedros (12)
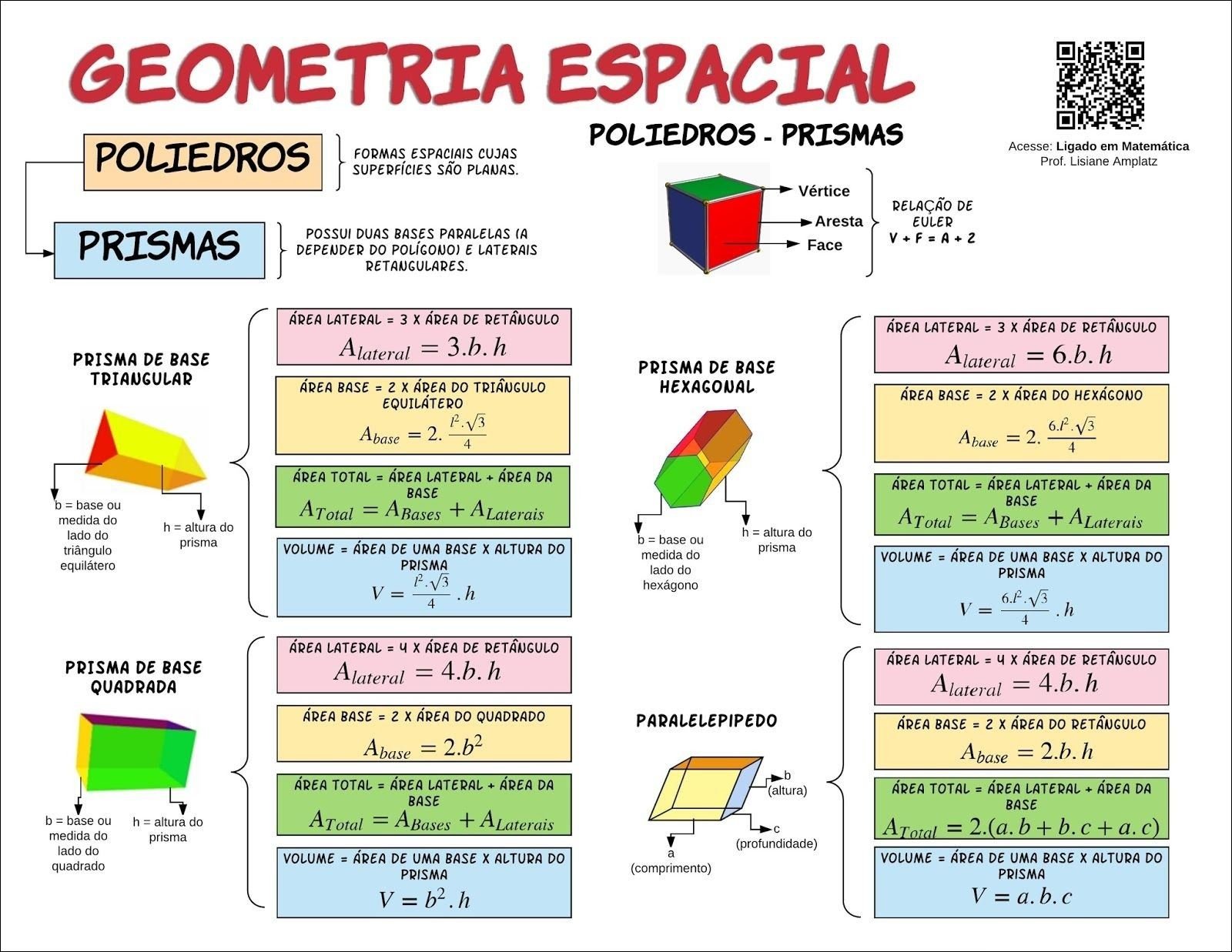
Mapa Mental sobre poliedros (13)
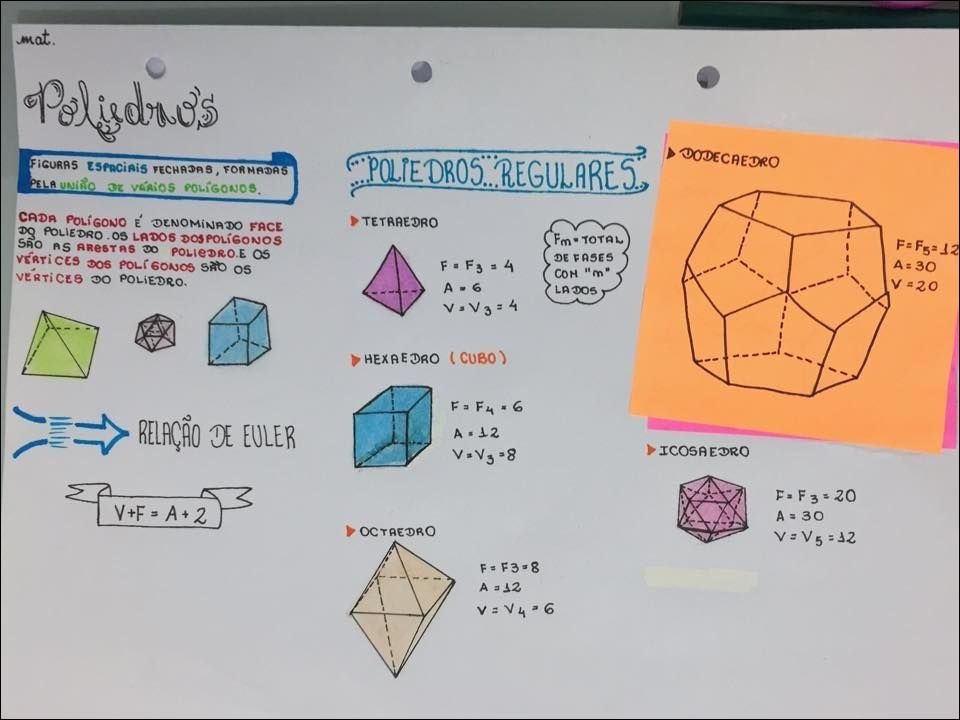
Mapa Mental sobre poliedros (14)
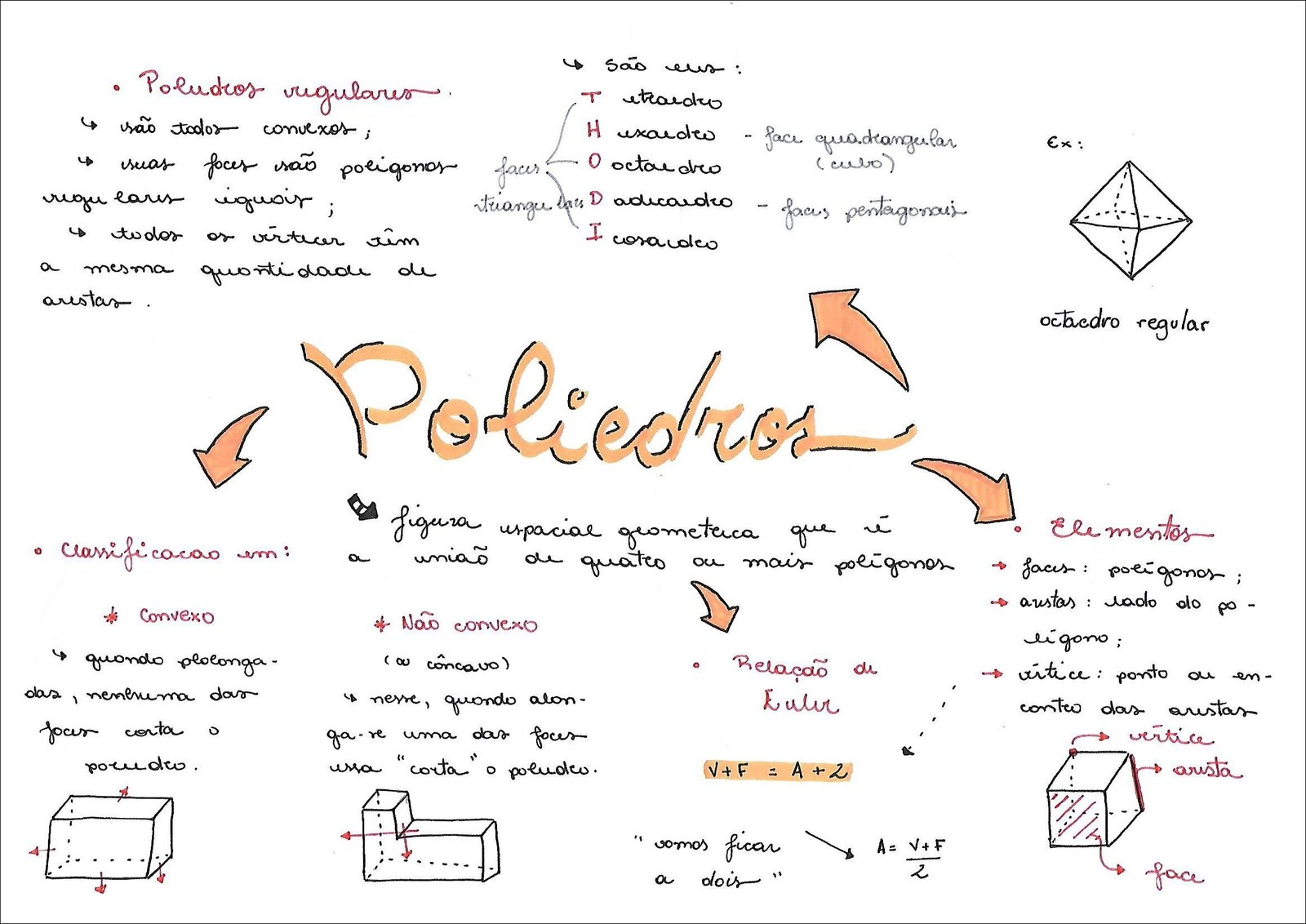
Mapa Mental sobre poliedros (15)

Mapa Mental sobre poliedros (16)

Mapa Mental sobre poliedros (17)

Mapa Mental sobre poliedros (18)
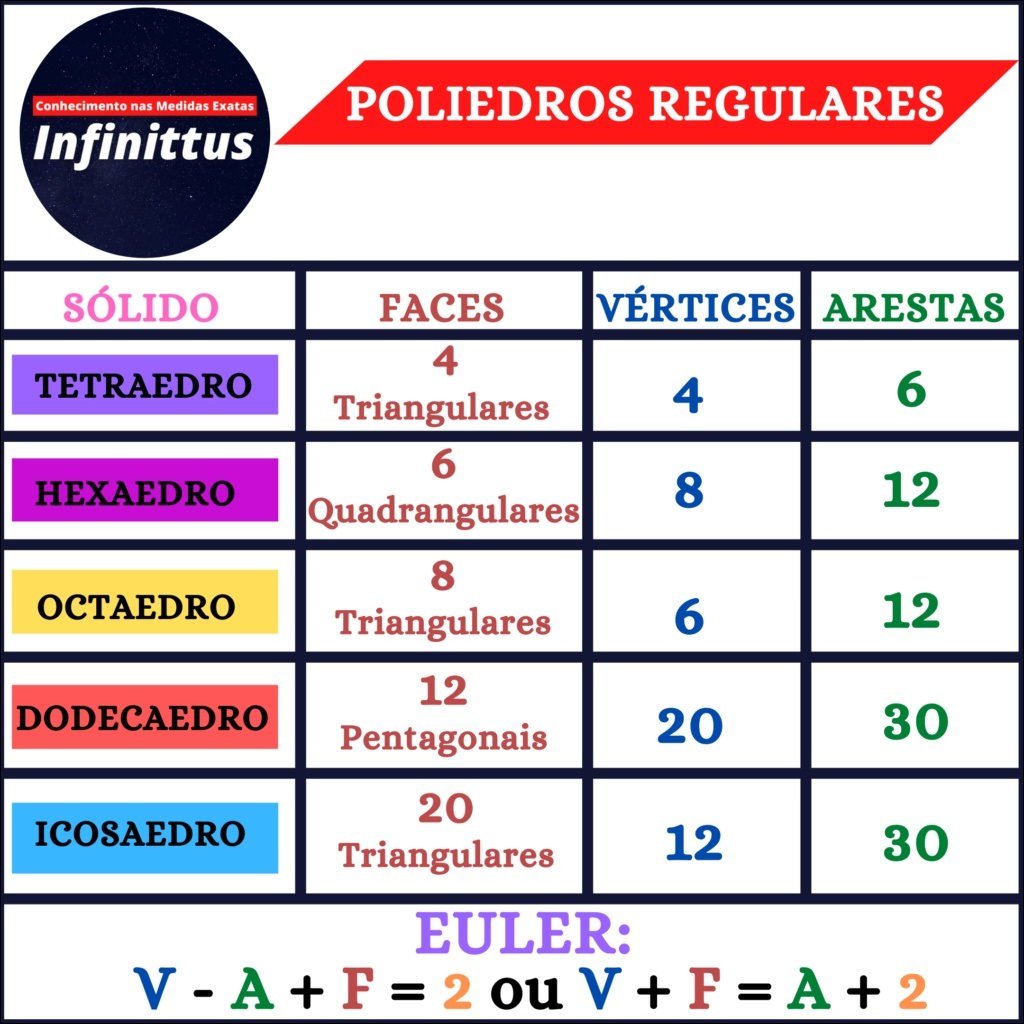
Mapa Mental sobre poliedros (19)
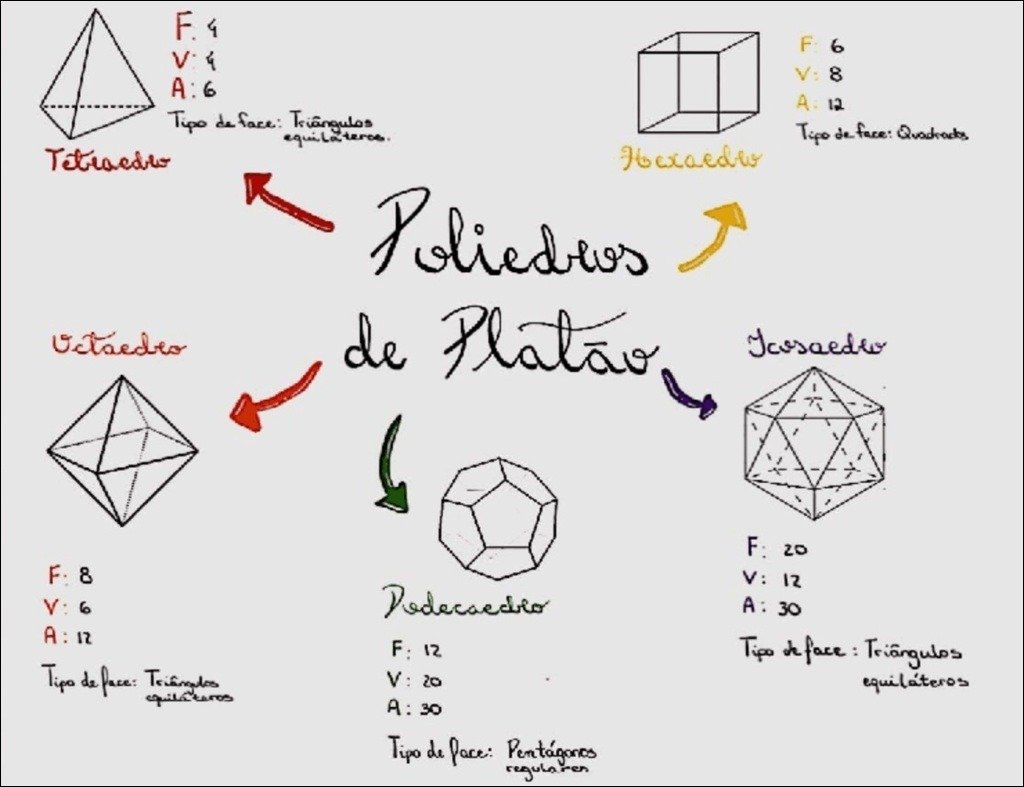
Mapa Mental sobre poliedros (20)
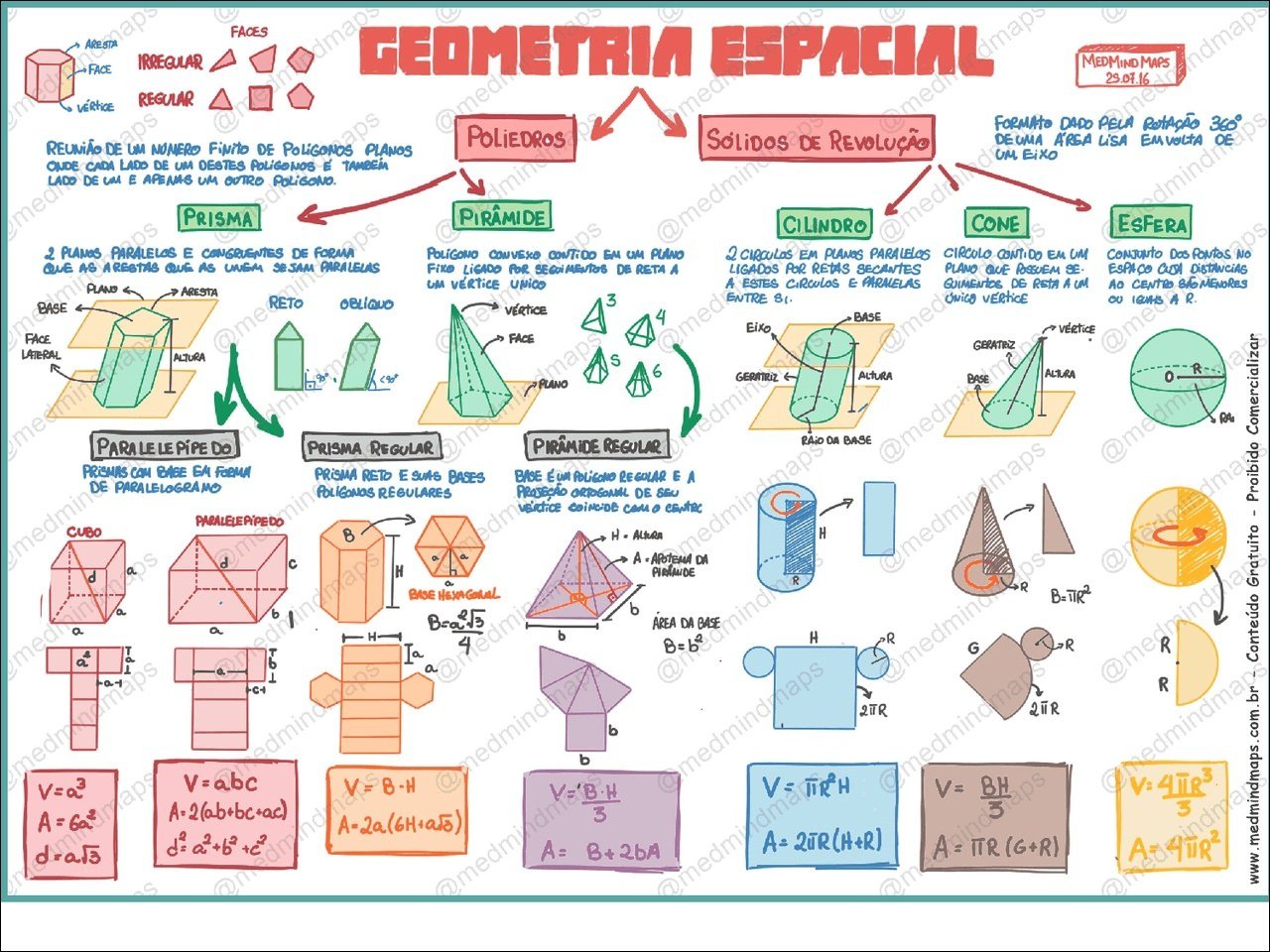
Resumo sobre poliedros
Poliedros: Uma Visão Geral
Poliedros são sólidos geométricos tridimensionais delimitados por faces planas, que são polígonos. A palavra “poliedro” deriva do grego “poly” (muitos) e “edron” (faces), refletindo sua característica fundamental de serem formados por múltiplas faces.
A estrutura de um poliedro é definida por suas faces, arestas e vértices. As faces são os polígonos que delimitam o sólido. As arestas são os segmentos de reta onde duas faces se encontram. Os vértices são os pontos onde as arestas se encontram, formando os cantos do poliedro.
Existem diversos tipos de poliedros, cada um com suas propriedades e características únicas. Os poliedros convexos são aqueles onde qualquer segmento de reta que conecta dois pontos dentro do sólido está inteiramente contido nele. Dentre eles, destacam-se os poliedros de Platão, que são os poliedros regulares com faces iguais e vértices congruentes, como o tetraedro, o cubo (hexaedro), o octaedro, o dodecaedro e o icosaedro.
Outros tipos importantes incluem os prismas, formados por duas bases poligonais idênticas e faces laterais paralelogramas, e as pirâmides, que têm uma base poligonal e faces laterais triangulares que convergem para um único vértice.
O estudo de poliedros é fundamental em diversas áreas, como geometria, arquitetura, design e ciência dos materiais. A compreensão de suas propriedades e classificações permite a análise e a construção de estruturas tridimensionais complexas, além de auxiliar na resolução de problemas relacionados a volume, área e relações espaciais.
